跳至主要内容

Normal 分佈的隨機生成器

假設我們現在有操作系統提供的 U(0,1)U(0,1) 随机数生成器。

Box-Muller 轉換​

U1,U2∼iidU(0,1)U_1, U_2 \stackrel{\text{iid}}{\sim} U(0,1) 且獨立，让

X=−2ln⁡U1cos⁡(2πU2)Y=−2ln⁡U1sin⁡(2πU2)\begin{align*} X &= \sqrt{-2 \ln U_1} \cos(2\pi U_2) \\ Y &= \sqrt{-2 \ln U_1} \sin(2\pi U_2) \end{align*}

則 X,Y∼iidN(0,1)X, Y \stackrel{\text{iid}}{\sim} N(0,1)。

基本原理​

这可以通过 Jacobian 计算得到。

∂(X,Y)∂(U1,U2)=∣−22U1−2ln⁡U1cos⁡(2πU2)−2ln⁡U1(−2πsin⁡(2πU2))−22U1−2ln⁡U1sin⁡(2πU2)−2ln⁡U1(2πcos⁡(2πU2))∣=−1U12πcos⁡2(2πU2)−1U12πsin⁡2(2πU2)=−2π1U1  ⟹  J=∂(U1,U2)∂(X,Y)=−U12π\begin{align*} &\begin{align*} \frac{\partial (X,Y)}{\partial (U_1, U_2)} &= \begin{vmatrix} \frac{-2}{2U_1\sqrt{-2\ln U_1}} \cos(2\pi U_2) & \sqrt{-2\ln U_1} (-2\pi \sin(2\pi U_2)) \\ \frac{-2}{2U_1\sqrt{-2\ln U_1}} \sin(2\pi U_2) & \sqrt{-2\ln U_1} (2\pi \cos(2\pi U_2)) \\ \end{vmatrix} \\ &= -\frac{1}{U_1} 2\pi \cos^2(2\pi U_2) - \frac{1}{U_1} 2\pi \sin^2(2\pi U_2) \\ &=-2\pi \frac{1}{U_1} \end{align*}\\ &\implies J = \frac{\partial (U_1, U_2)}{\partial (X,Y)} =-\frac{U_1}{2\pi} \end{align*}

均勻分佈的機率在有效區間內是常數，所以我們不需要關心 U1,U2U_1,U_2 的反函數，但 JJ 還是有包含 U1U_1，因此我們還是需要計算得到 U1=exp⁡X2+Y2−2U_1=\exp{\frac{X^2+Y^2}{-2}}，

f(X,Y)(x,y)=f(U1,U2)(g1(x,y),g2(x,y))∣J∣=12πexp⁡X2+Y2−2=12πexp⁡X2−212πexp⁡Y2−2f_{(X,Y)}(x,y)=f_{(U_1,U_2)}(g_1(x,y), g_2(x,y))|J| = \frac{1}{2\pi} \exp{\frac{X^2+Y^2}{-2}} = \frac{1}{\sqrt{2\pi}} \exp{\frac{X^2}{-2}} \frac{1}{\sqrt{2\pi}} \exp{\frac{Y^2}{-2}}

得到了兩個獨立的 normal 分佈的聯合概率密度函數，因此 X,Y∼iidN(0,1)X, Y\stackrel{\text{iid}}{\sim} N(0,1) 獨立。

以 U1U_1 为例，可以把 U1U_1 看做是 U1=Rcos⁡(θ)U_1=R\cos(\theta)。其中 θ∼iidU(0,2π)\theta\stackrel{\text{iid}}{\sim} U(0,2\pi) ，相当于是均匀的选取一个角度。而 R2=−2ln⁡U1R^2=-2\ln U_1 服从卡方分布 χ22\chi^2_2。

Z12+Z22=χ22=−2ln⁡U=−2ln⁡U(cos⁡2θ+sin⁡2θ)Z_1^2+Z_2^2 = \chi^2_2 = -2\ln U = -2\ln U (\cos^2\theta+\sin^2\theta)

代碼實現​

use rand::distributions::Standard;
use rand::prelude::*;
use std::f64::consts::PI;

fn box_muller() -> f64 {
    let mut u1: f64 = StdRng::from_entropy().sample(Standard);
    let mut u2: f64 = StdRng::from_entropy().sample(Standard);
    while u1 == 0.0 {
        u1 = StdRng::from_entropy().sample(Standard);
    }

    while u2 == 0.0 {
        u2 = StdRng::from_entropy().sample(Standard);
    }

    let z1 = (-2.0_f64 * u1.ln()).sqrt() * (2.0 * PI * u2).cos();
    return z1;
}

Ziggurat 算法​

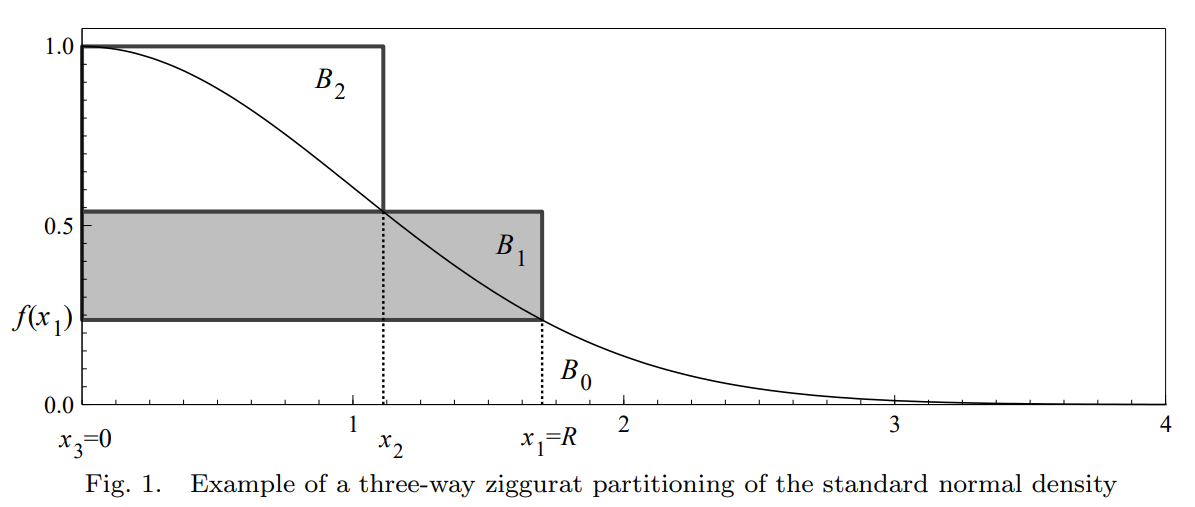
Ziggurat 算法是一種採樣拒絕類的算法。它的基本思想是在平面上畫一個分佈函數的曲線，然後在曲線下隨機生成一個點。幾率高的地方，其曲線下方擁有更多的面積，因此點落在這些地方的概率也更大。因為本身就是以曲線為單位隨機生成點，因此在繪製曲線時可以省略標準化，比如 N(0,1)N(0,1) 可以使用 f(x)=exp⁡(−x2/2)f(x)=\exp(-x^2/2) 作為曲線函數。

為了加快運行速度，Ziggurat 算法實際上是用許多矩形來逼近分佈函數的圖形，而這些矩形的坐標可以提前計算並儲存，這在生成大量隨機數時可以大大提高效率。

alt text

算法假設每個矩形的面積都相同，因此隨機生成的點落在每個矩形的幾率應該是相同的。反過來了，當要隨機生成一個點時，我們可以先公平地隨機選一個矩形，然後再在這個矩形中生成一個點。

從示意圖上可以注意到，矩形可以被分為兩個部分：完全處在曲線下方和部分處在曲線下方。在選擇好矩形後（如圖中 B1B_1），首先生成一個 xx 座標，服從 U(0,x1)U(0,x_1)。如果 x<x2x<x_2，那麼無論 yy 的值如何，這個點都一定處在曲線下方，因此可以直接接受。如果落在第二部分，則需要生成一個服從 U(f(x1),f(x2))U(f(x_1),f(x_2)) 的 yy 座標，如果 y<f(x)y<f(x)，則接受，否則拒絕這個點並重新生成。

無論矩形的數量如何，尾部總會有無法被完全覆蓋的部分（如圖中 x1x_1 右側部分）。當點落在這個部分時，則需要使用其他方式來驗證這個點是否在曲線下方。由於這部分的面積很小，因此可以選擇較慢的方法。

計算矩形​

假設我們首先設定了每個矩形的面積都為 VV，其中最下方的 B0B_0 為矩形部分和尾部曲線組成。

x2[f(x3)−f(x2)]=x1[f(x2)−f(x1)]=x1f(x1)+∫x1∞f(x)dx=Vx_2[f(x_3)-f(x_2)] = x_1[f(x_2)-f(x_1)] = x_1f(x_1) + \int_{x_1}^{\infty}f(x)dx=V

如果最右的 x1x_1 也已經提供，那麼後續的點 x2x_2 可以通過 VV 和 f(x1)f(x_1) 來計算：

x2=f−1(f(x1)+V/x1)x_2 = f^{-1}(f(x_1) + V/x_1)

如果我們要用 CC 個矩形來逼近，令 xC=0x_C=0，而前 C−1C-1 個矩形的 xx 座標可以通過遞推得到：

xi=f−1(f(xi−1)+V/xi−1),i=2,⋯ ,C−1x_i = f^{-1}(f(x_{i-1}) + V/x_{i-1}),\quad i=2,\cdots,C-1

可以從看出 xix_i 實際上會隨著 VV 改變，而 VV 其實是 x1x_1 的函數。因此，分割的關鍵在於如何確定 x1x_1。

xC−1(x1)[f(xC)−f(xC−1(x1))]=V(x1)x_{C-1}(x_1)[f(x_C)-f(x_{C-1}(x_1))] = V(x_1)

通過數值方法找到以上方程的解，就可以得到 x1x_1 的值。