Hashlife(Game of life)
生命遊戲是一個在二維網格上,根據一定規則自動演化的生命模擬遊戲。每個格子有兩個狀態:活著或死亡。每個格子的狀態取決於其周圍八個格子的狀態。生命遊戲的規則如下:
- 活著的格子,如果周圍有2個或3個活著的格子,則下一代繼續活著;否則死亡。
- 死亡的格子,如果周圍有3個活著的格子,則下一代變成活著;否則繼續死亡。
- 其他情況下,下一代的狀態和當前狀態相同。
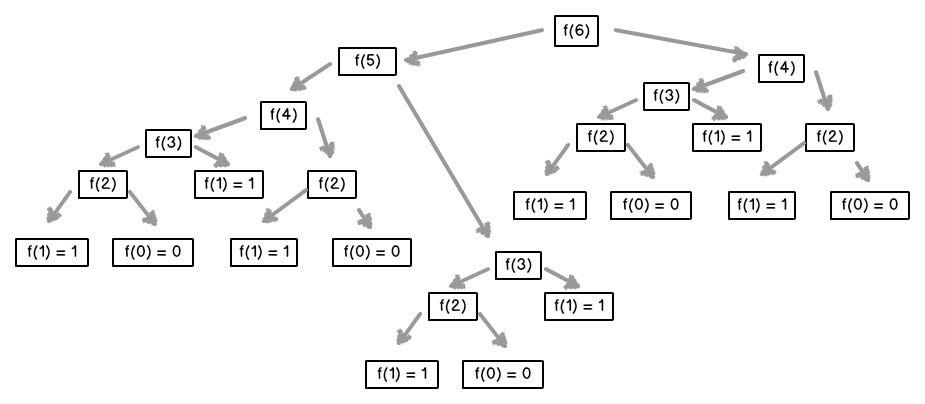
Hashlife 是一種基於遞迴和哈希表緩存的高效算法。因為生命遊戲往往有大量重複的狀態,Hashlife 通過哈希表緩存已經計算過的狀態,避免重複計算,從而提高計算效率。

Hashlife 通過將自身平均分割成四個子網格,每個子網格的邊長是原網格的一半,來實現遞迴計算。因此,棋盤的邊長必須是2的冪次方。
思路
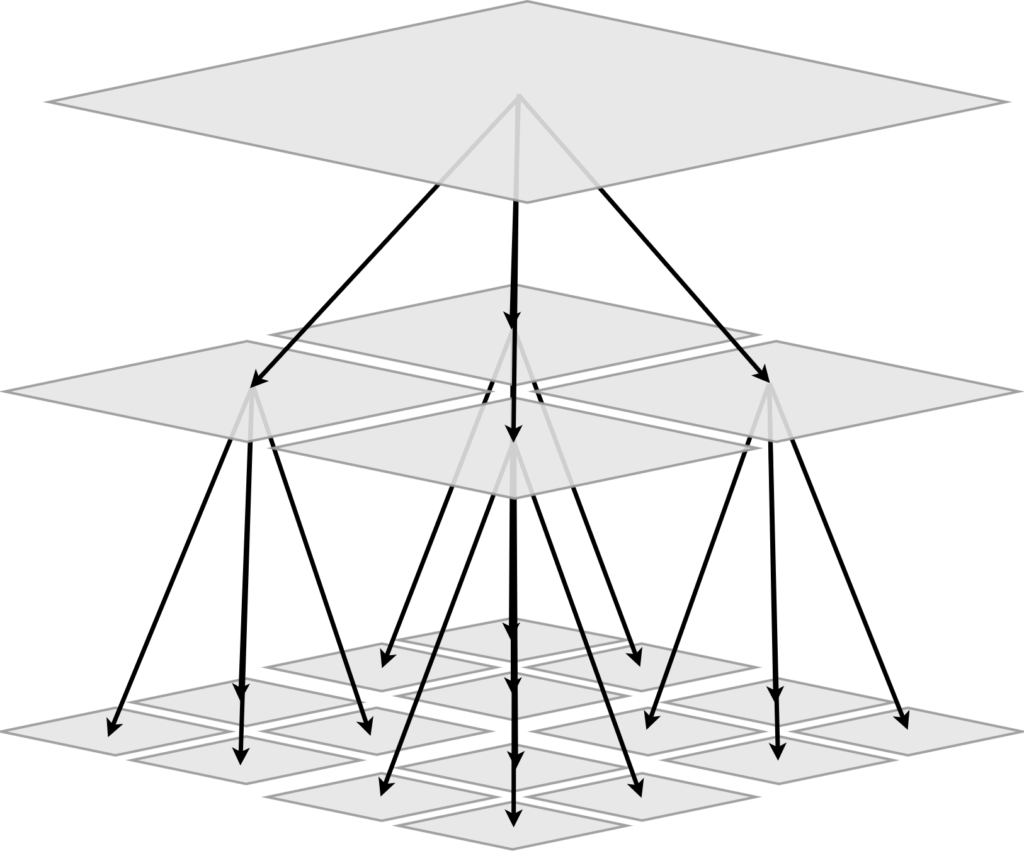
棋盤本身是一個最大的節點(Node),每個節點包含了四個子節點,直到細分為 1x1 的節點,也就是棋盤上的一個格子,儲存了格子的狀態(bool)。
假設每個節點有 level 屬性,表示節點的層級,同樣代表節點的邊長為 2^level。而四個子節點的層級則是 level - 1。
因為遞回算法的性質,導致每個節點計算下一代時並不知道周圍的狀態,因此每個節點只能計算中心的狀態。而這中心的狀態本身可以形成一個層級為 level - 1 的節點。因此,我們可以通過子節點的狀態來計算父節點的狀態。
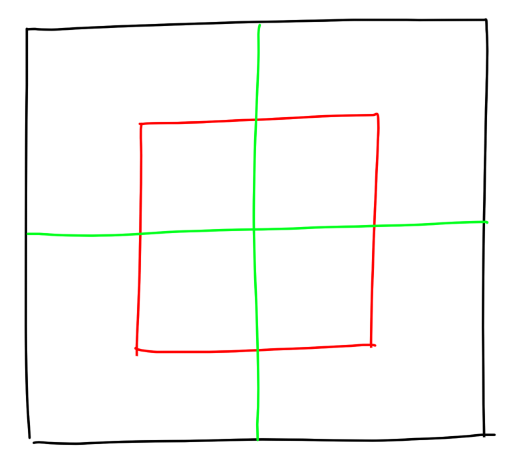
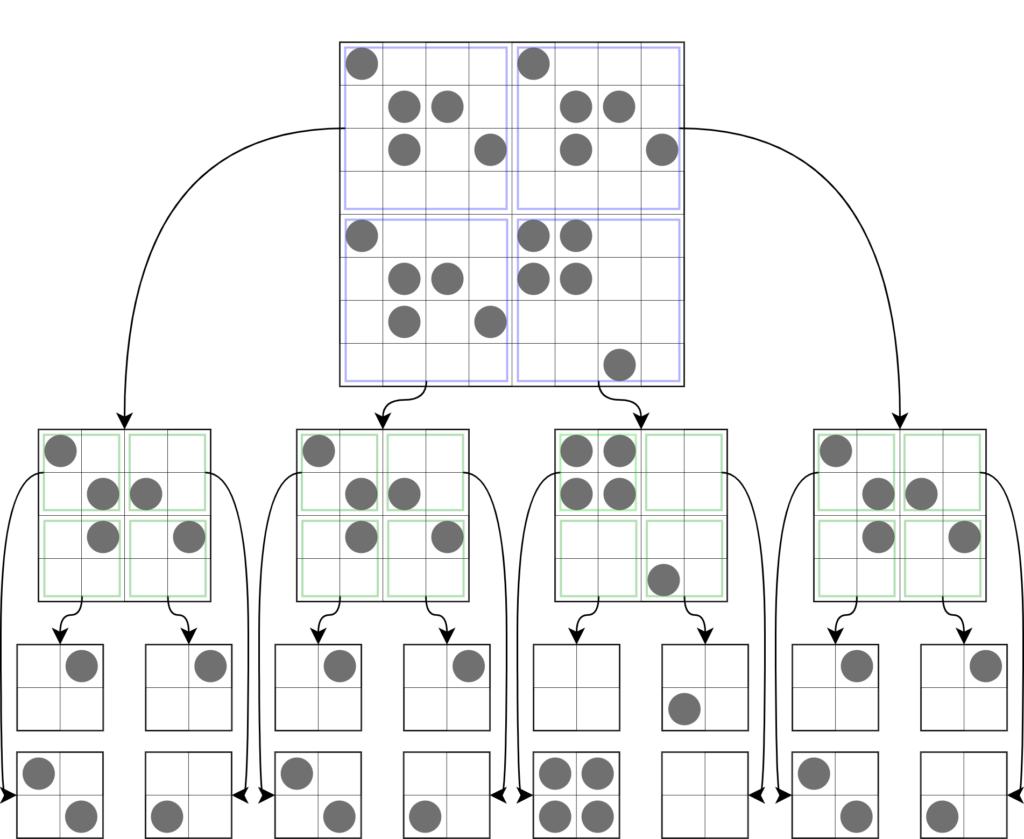
我們先假設 level - 1 層級的節點都已經實現了 next() 方法用以計算下一代的狀態,並且返回節點的層級為 level - 2。但當前節點還沒有實現 next() 方法。我們可以通過調用子節點的 next() 方法來實現當前節點的 next() 方法。也就是我們現在需要用下一代的狀態拼出紅色部分的節點。
紅色的節點同樣也由 4 個子節點組成。以左上角子節點舉例,他可以由藍色節點執行 next() 方法得到。以此類推,我們需要組成 4 個 level - 1 的節點,並分別調用它們的 next() 方法,得到 4 個 level - 2 的節點。最後,我們再將這 4 個 level - 2 的節點組合成一個 level - 1 的節點,並返回。
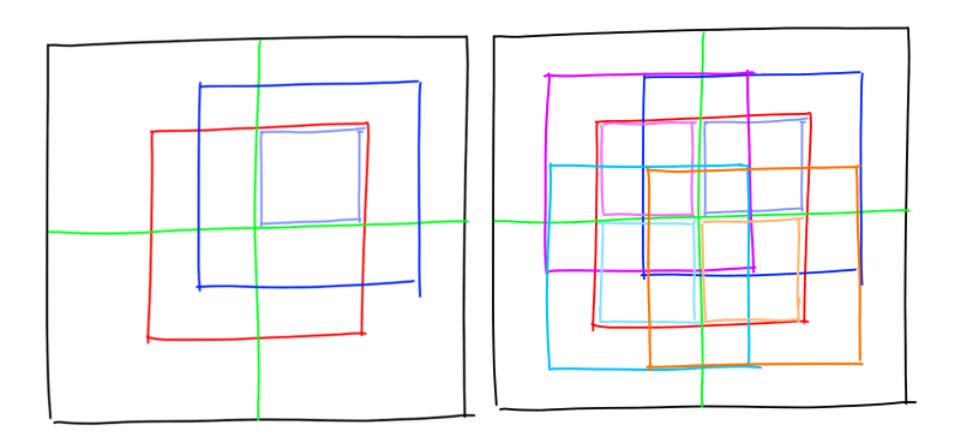
為了方便的創建 4 個 level - 1 的節點,我們可以創建 9 個 level - 2 的輔助節點。其中 n00,n02,n20,n22 是子節點的子節點,n01 和 n21 需要通過水平整合兩個子節點得到,n10 和 n12 需要通過垂直整合兩個子節點得到。n11 需要整合 4 個子節點得到。
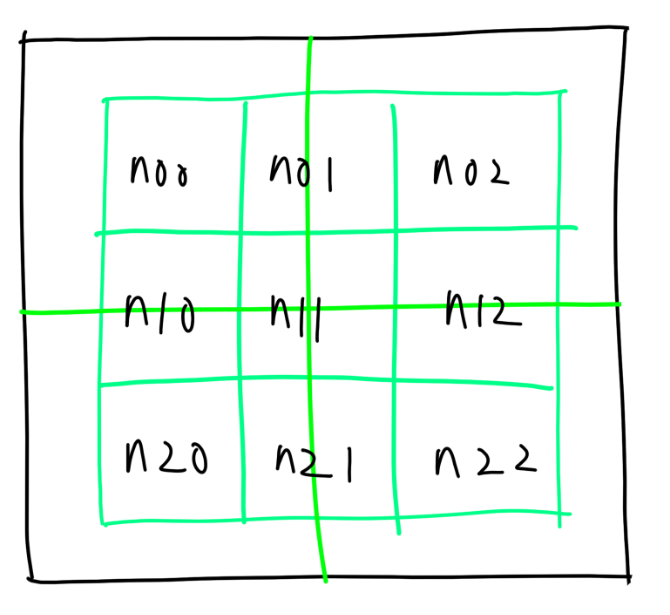
通過以上描述可以觀察到,這個遞回過程最少需要向下訪問 2 曾節點。因此,算法最少需要 level=3 的節點。而對於 level=2,也就是邊長為 4 的節點,我們則直接根據遊戲規則計算出中間 2x2 的節點的狀態,並返回 level=1 的節點。
以上是遞回算法的基本思路。接下來我們可以維護一個 hash 表,用以緩存已經計算過的節點。每次調用 next() 時,我們會先查詢表,如果已經計算過,則直接返回。否則,我們用上述的遞回算法計算出下一代的狀態,並將結果存入 hash 表。
因為生命遊戲可能會出現重複的模式,這代表可能會有多個一樣結構的節點。因此在儲存方面,我們不需要儲存原始的節點,而是可以儲存節點的指針。這樣可以節省空間。
問題
在算法計算的過程中,因為已經將已經計算過的狀態緩存,因此計算的速度是很快的。而瓶頸則在於 hash 算法的實現。尤其是計算 hash 的過程同樣需要遞回計算,因此需要一個高效的 hash 算法。否則仍然會出現遞回 fibonacci 數列的問題。只是不是在計算生命遊戲的過程中,而是在計算 hash 的過程中。