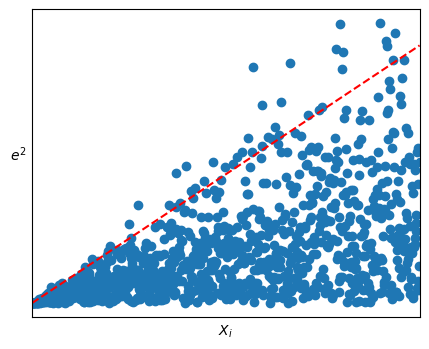
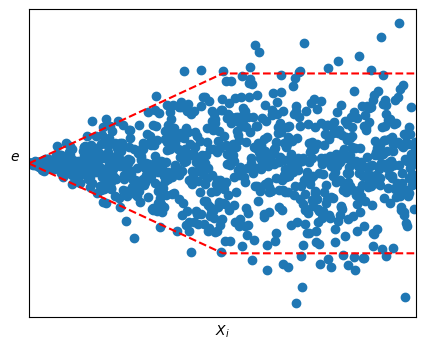
模型的診斷與補救(Diagnostic/Remedial techniques) 以往的推論,都是基於以下假設:
ε ~ ∼ N ( 0 , σ 2 I ) E ( y ~ ) = D β ~ \utilde{\varepsilon}\sim N(0,\sigma^2I)\qquad E(\utilde{y})=D\utilde{\beta} ε ∼ N ( 0 , σ 2 I ) E ( y ) = D β 但是,收集到的數據並不一定符合這些假設。因此,在通過統計報表得到結論之前,我們需要檢查模型是否適合這筆數據。這種檢查稱為模型診斷(diagnostics)。
Remark : 通常會使用殘差 e i = y i − y ^ i e_i=y_i-\hat{y}_i e i = y i − y ^ i
Idea : 當模型正確的時候,我們可以推導出殘差應該符合的性質。因此,如果殘差圖嚴重違反這些性質,那麼我們就可以認為模型不適合數據。如果模型並沒有嚴重違背,那麼我們就可以認為模型適合這些數據。
任何模型都是錯誤的,但有些模型是有用的。因此,我們不應該追求完美的模型,而是應該追求有用的模型。
首先第一個問題,為什麼用殘差來診斷模型是否適合數據?
一般來說,在設計模型時,我們會讓設計矩陣 D D D ( D t D ) t (D^tD)^t ( D t D ) t ⟹ Y ^ ~ = H Y ~ \implies \utilde{\hat{Y}}=H\utilde{Y} ⟹ Y ^ = H Y H = D ( D t D ) − 1 D t H=D(D^tD)^{-1}D^t H = D ( D t D ) − 1 D t
⟹ e ~ = Y ~ − Y ^ ~ = ( I − H ) Y ~ = M Y ~ = d M ( D β ~ + ε ~ ) = M ε ~ = ( I − H ) ε ~ \begin{align*}
\implies \utilde{e}&=\utilde{Y}-\utilde{\hat{Y}}=(I-H)\utilde{Y}=M\utilde{Y}\overset{\text{d}}{=}M(D\utilde{\beta}+\utilde{\varepsilon})\\
&=M\utilde{\varepsilon}=(I-H)\utilde{\varepsilon}
\end{align*} ⟹ e = Y − Y ^ = ( I − H ) Y = M Y = d M ( D β + ε ) = M ε = ( I − H ) ε 這裡 e ~ , Y ^ ~ , Y ~ \utilde{e}, \utilde{\hat{Y}}, \utilde{Y} e , Y ^ , Y M ( D β ~ + ε ~ ) M(D\utilde{\beta}+\utilde{\varepsilon}) M ( D β + ε ) = = = = d \overset{\text{d}}{=} = d
Y ~ = D β ~ + ε ~ \utilde{Y}=D\utilde{\beta}+\utilde{\varepsilon} Y = D β + ε Y ~ \utilde{Y} Y Y ~ \utilde{Y} Y
如果 ε ~ ∼ N n ( 0 , σ 2 I ) ⟹ e ~ ∼ N n ( 0 , σ 2 ( I − H ) ) \utilde{\varepsilon}\sim N_n(0, \sigma^2I)\implies\utilde{e}\sim N_n(0, \sigma^2(I-H)) ε ∼ N n ( 0 , σ 2 I ) ⟹ e ∼ N n ( 0 , σ 2 ( I − H ))
令 H = ( h 1 ~ , ⋯ , h n ~ ) ⟹ e ~ = d ( I − H ) ε ~ = ε ~ − H ε ~ H=(\utilde{h_1},\cdots,\utilde{h_n})\implies \utilde{e}\overset{\text{d}}{=}(I-H)\utilde{\varepsilon}=\utilde{\varepsilon}-H\utilde{\varepsilon} H = ( h 1 , ⋯ , h n ) ⟹ e = d ( I − H ) ε = ε − H ε
∀ i e i = d ε i − h i ~ t ε ~ = ε i − ∑ j = 1 n h i j ε j ( △ 1 ) \forall i\quad e_i\overset{\text{d}}{=}\varepsilon_i-\utilde{h_i}^t\utilde{\varepsilon}=\varepsilon_i-\sum_{j=1}^n h_{ij}\varepsilon_j\tag{$\triangle_1$} ∀ i e i = d ε i − h i t ε = ε i − j = 1 ∑ n h ij ε j ( △ 1 )
E ( e i ) = 0 E(e_i)=0 E ( e i ) = 0 σ 2 { e i } = ( 1 − h i i ) σ 2 \sigma^2\set{e_i}=(1-h_{ii})\sigma^2 σ 2 { e i } = ( 1 − h ii ) σ 2
Note that H H = H , H t = H HH=H, H^t=H HH = H , H t = H h i i = h i ~ t h i ~ , ∀ i h_{ii}=\utilde{h_i}^t\utilde{h_i},\forall i h ii = h i t h i , ∀ i
E ( h t ~ ε ~ ) = 0 E(\utilde{h^t}\utilde{\varepsilon})=0 E ( h t ε ) = 0 σ 2 { h i t ~ ε ~ } = h i t ~ σ 2 { ε ~ h i ~ } = σ 2 h i i \sigma^2\set{\utilde{h_i^t}\utilde{\varepsilon}}=\utilde{h_i^t}\sigma^2\set{\utilde{\varepsilon}\utilde{h_i}}=\sigma^2h_{ii} σ 2 { h i t ε } = h i t σ 2 { ε h i } = σ 2 h ii
如果 h i i ≈ 0 ⟹ σ 2 { h i t ~ ε ~ } ≈ 0 h_{ii}\approx 0\implies\sigma^2\set{\utilde{h_i^t}\utilde{\varepsilon}}\approx 0 h ii ≈ 0 ⟹ σ 2 { h i t ε } ≈ 0 Chebyshev's inequality ,如果方差很小,那麼這個隨機變量就會很接近於常��數,並且這個常數會是它的期望值。i.e. h i t ~ ε ~ ≈ E ( h i t ~ ε ~ ) = 0 \utilde{h_i^t}\utilde{\varepsilon}\approx E(\utilde{h_i^t}\utilde{\varepsilon})=0 h i t ε ≈ E ( h i t ε ) = 0 ( △ 1 ) (\triangle_1) ( △ 1 ) e i ≈ d ε i e_i\overset{\text{d}}{\approx}\varepsilon_i e i ≈ d ε i
因此,當 h i i ≈ 0 h_{ii}\approx 0 h ii ≈ 0 e i e_i e i ε i \varepsilon_i ε i
c.f. ε ~ \utilde{\varepsilon} ε e ~ \utilde{e} e
∑ e i = 0 \sum e_i=0 ∑ e i = 0 n − 1 n-1 n − 1 n n n σ 2 { e ~ } = σ 2 ⋅ M \sigma^2\set{\utilde{e}}=\sigma^2\cdot M σ 2 { e } = σ 2 ⋅ M M M M
接下來的問題是 h i i h_{ii} h ii
∀ i 0 ≤ h i i = h i ~ t h i ~ = ∑ j = 1 n h i j 2 = h i i 2 + ∑ j ≠ i h i j ≥ h i i 2 \forall i\quad 0\le h_{ii}=\utilde{h_i}^t\utilde{h_i}=\sum_{j=1}^n h_{ij}^2=h_{ii}^2+\sum_{j\neq i}h_{ij}\ge h_{ii}^2 ∀ i 0 ≤ h ii = h i t h i = j = 1 ∑ n h ij 2 = h ii 2 + j = i ∑ h ij ≥ h ii 2 ⟹ h i i ∈ [ 0 , 1 ] \implies h_{ii}\in[0,1] ⟹ h ii ∈ [ 0 , 1 ] rank ( H ) = dim ( Ω ) = p = tr ( H ) = ∑ i = 1 n h i i \text{rank}(H)=\dim(\Omega)=p=\text{tr}(H)=\sum_{i=1}^n h_{ii} rank ( H ) = dim ( Ω ) = p = tr ( H ) = ∑ i = 1 n h ii
因此 h i i h_{ii} h ii p n \frac{p}{n} n p n ≫ p n\gg p n ≫ p p n ≈ 0 ⟹ h i i ≈ 0 ⟹ ∑ j = 1 n h i j 2 ≈ 0 ⟹ h i j ≈ 0 \frac{p}{n}\approx 0\implies h_{ii}\approx 0\implies\sum_{j=1}^nh_{ij}^2\approx 0\implies h_{ij}\approx 0 n p ≈ 0 ⟹ h ii ≈ 0 ⟹ ∑ j = 1 n h ij 2 ≈ 0 ⟹ h ij ≈ 0 ∀ j ≠ i \forall j\neq i ∀ j = i
此時 M M M e ~ \utilde{e} e M M M 1 1 1 n n n
e i ∼ N ( 0 , ( 1 − h i i ) σ 2 ) e_i\sim N(0,(1-h_{ii})\sigma^2) e i ∼ N ( 0 , ( 1 − h ii ) σ 2 )
standardized residual:
γ i ≜ e i MSE ( 1 − h i i ) ∼ t n − p → n − p → ∞ N ( 0 , 1 ) \gamma_i\triangleq\frac{e_i}{\sqrt{\text{MSE}(1-h_{ii})}}\sim t_{n-p}\xrightarrow[n-p\to\infty]{} N(0,1) γ i ≜ MSE ( 1 − h ii ) e i ∼ t n − p n − p → ∞ N ( 0 , 1 )
n ≫ p n\gg p n ≫ p h i i = 0 h_{ii}=0 h ii = 0
e ~ i ∗ ≜ e i MSE ∼ : N ( 0 , 1 ) \utilde{e}^*_i\triangleq\frac{e_i}{\sqrt{\text{MSE}}}\simcolon N(0,1) e i ∗ ≜ MSE e i ∼ : N ( 0 , 1 )
i.e.
n ≫ p ⟹ { γ 1 , ⋯ , γ n e 1 ∗ , ⋯ , e n ∗ sample of size n from N ( 0 , 1 ) n\gg p \implies\begin{cases}
\gamma_1,\cdots,\gamma_n\\
e^*_1,\cdots,e^*_n
\end{cases}\quad\text{ sample of size }n\text{ from }N(0,1) n ≫ p ⟹ { γ 1 , ⋯ , γ n e 1 ∗ , ⋯ , e n ∗ sample of size n from N ( 0 , 1 ) 殘差圖
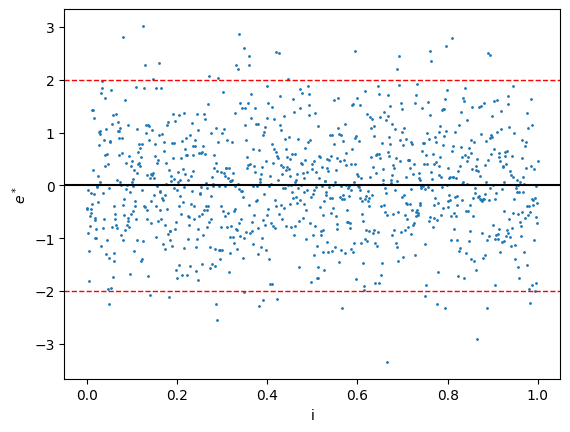
在做診斷時,我們通常會畫出殘差圖(residual plot)來檢查模型是否適合數據。因為 e i e_i e i σ \sigma σ e i ∗ e^*_i e i ∗ γ i \gamma_i γ i
殘差直方圖
因為理想狀況下我們認為殘差是服從期望值為 0 0 0 0 0 0
理想:
非理想:
要注意的是,當數據量少的時候,殘差的直方圖可能並不會呈現完美的常態分佈。在這種情況,我們可以直接把點畫出來,然後看是否集中於 0 0 0
時間序列圖(Time sequence plot)
因為 e ~ \utilde{e} e ε ~ \utilde{\varepsilon} ε ε ~ \utilde{\varepsilon} ε e i e_i e i i i i
理想狀況下,e i / e i ∗ / γ i e_i/e^*_i/\gamma_i e i / e i ∗ / γ i i i i
如果點圖畫出來發現有線性或非線性的趨勢,那麼 i i i
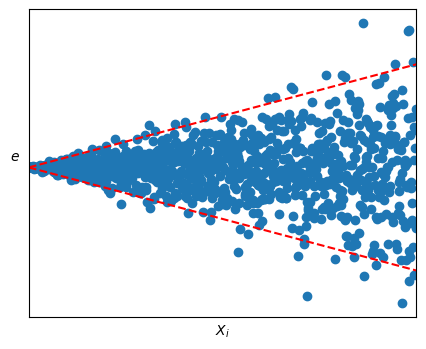
而如果殘差圖的波動範圍有明顯變化,這代表數據違背了方差相等的假設。這可以通過做加權最小二乘法(WLSE)或通過轉換來解決。
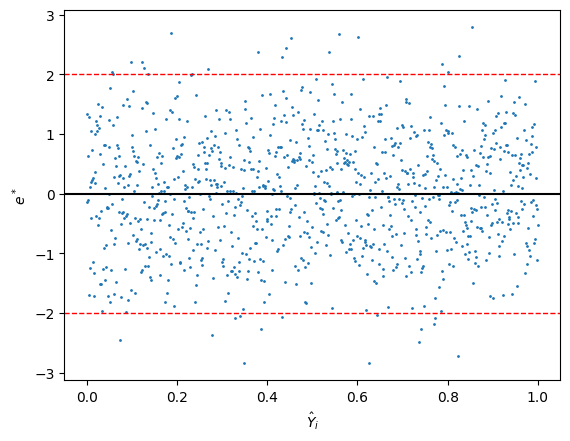
e i / e i ∗ / γ i e_i/e^*_i/\gamma_i e i / e i ∗ / γ i Y ^ i \hat{Y}_i Y ^ i
e i / e i ∗ / γ i e_i/e^*_i/\gamma_i e i / e i ∗ / γ i x x x
理想下,這個圖同樣也會是呈現一條在 x 軸附近的水平區帶。
非理想下:
呈線性關係:這代表代碼可能有問題。如果 x x x x x x
曲線關係:
可能需要在模型中加入額外的變數,e.g. x 2 x^2 x 2
對 Y i Y_i Y i
波動範圍有明顯變化:
通過做加權最小二乘法(WLSE)
通過對 Y i Y_i Y i
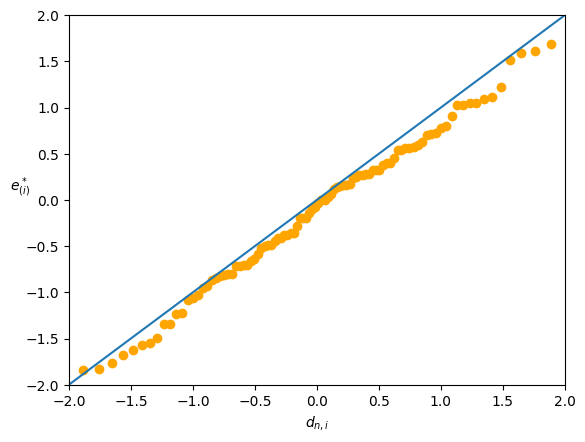
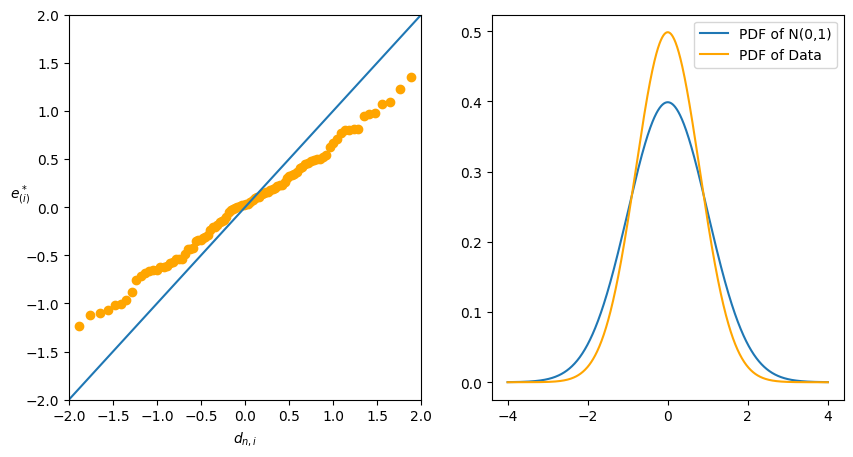
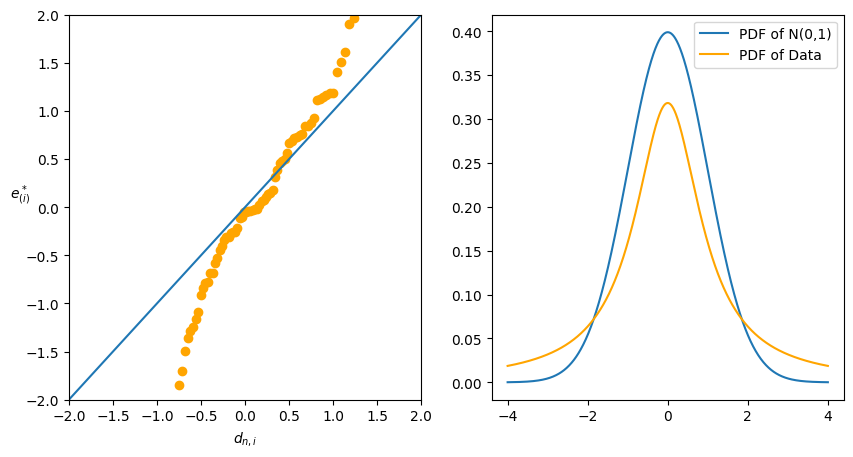
Normal probability plot(Normal Quantile-Quantile Plot)
理想下,q-q plot 畫出來的圖應該是直線的。
Note:U 1 , ⋯ , U n ∼ U ( 0 , 1 ) U_1,\cdots,U_n\sim U(0,1) U 1 , ⋯ , U n ∼ U ( 0 , 1 ) U ( 1 ) ≤ ⋯ ≤ U ( n ) U_{(1)}\le\cdots\le U_{(n)} U ( 1 ) ≤ ⋯ ≤ U ( n )
pdf of U ( i ) = n ! ( i − 1 ) ! ( n − i ) ! t i − 1 ( 1 − t ) n − i t ∈ ( 0 , 1 ) \text{pdf of }U_{(i)}=\frac{n!}{(i-1)!(n-i)!}t^{i-1}(1-t)^{n-i}\quad t\in(0,1) pdf of U ( i ) = ( i − 1 )! ( n − i )! n ! t i − 1 ( 1 − t ) n − i t ∈ ( 0 , 1 ) ⟹ U ( i ) ∼ Beta ( i , n − i + 1 ) \implies U_{(i)}\sim \text{Beta}(i,n-i+1) ⟹ U ( i ) ∼ Beta ( i , n − i + 1 ) E ( U ( i ) ) = i n + 1 E(U_{(i)})=\frac{i}{n+1} E ( U ( i ) ) = n + 1 i
U ( i ) = E ( U ( i ) ) + U ( i ) − E ( U ( i ) ) = i n + 1 + ε i ∗ where E ( ε i ∗ ) = 0 \begin{align*}
U_{(i)}&=E(U_{(i)})+U_{(i)}-E(U_{(i)})\\
&=\frac{i}{n+1}+\varepsilon^*_i\quad\text{where } E(\varepsilon^*_i)=0
\end{align*} U ( i ) = E ( U ( i ) ) + U ( i ) − E ( U ( i ) ) = n + 1 i + ε i ∗ where E ( ε i ∗ ) = 0 因此這就會是一個簡單線性回歸模型。
Recall: 如果隨機變量 W W W F F F F ( W ) ∼ U ( 0 , 1 ) F(W)\sim U(0,1) F ( W ) ∼ U ( 0 , 1 )
令 W 1 , ⋯ , W n ∼ iid N ( μ , τ 2 ) W_1,\cdots,W_n\overset{\text{iid}}{\sim} N(\mu,\tau^2) W 1 , ⋯ , W n ∼ iid N ( μ , τ 2 ) W ( 1 ) ≤ ⋯ ≤ W ( n ) W_{(1)}\le\cdots\le W_{(n)} W ( 1 ) ≤ ⋯ ≤ W ( n )
W i − μ τ ∼ N ( 0 , 1 ) ⟹ Φ ( W i − μ τ ) ∼ U ( 0 , 1 ) \frac{W_i-\mu}{\tau}\sim N(0,1)\implies\Phi\left(\frac{W_i-\mu}{\tau}\right)\sim U(0,1) τ W i − μ ∼ N ( 0 , 1 ) ⟹ Φ ( τ W i − μ ) ∼ U ( 0 , 1 ) 因為 Φ \Phi Φ
∴ Φ ( W ( i ) − μ τ ) ∼ Beta ( i , n − i + 1 ) ⟹ E ( Φ ( W ( i ) − μ τ ) ) = i n + 1 \therefore \Phi\left(\frac{W_{(i)}-\mu}{\tau}\right)\sim \text{Beta}(i,n-i+1)\implies E\left(\Phi\left(\frac{W_{(i)}-\mu}{\tau}\right)\right)=\frac{i}{n+1} ∴ Φ ( τ W ( i ) − μ ) ∼ Beta ( i , n − i + 1 ) ⟹ E ( Φ ( τ W ( i ) − μ ) ) = n + 1 i Idea: 如果 X X X Φ ( X ) \Phi(X) Φ ( X ) E [ X ] E[X] E [ X ]
Φ ( X ) ≈ Φ ( E [ X ] ) + ϕ ( E [ X ] ) ( X − E [ X ] ) ⟹ E [ Φ ( X ) ] ≈ Φ ( E [ X ] ) + E [ ϕ ( E [ X ] ) ] ( E [ X ] − E [ X ] ) = E [ Φ ( X ) ] \begin{align*}
&\Phi(X)\approx \Phi(E[X])+\phi(E[X])(X-E[X])\\
\implies& E[\Phi(X)]\approx \Phi(E[X])+E[\phi(E[X])](E[X]-E[X])=E[\Phi(X)]
\end{align*} ⟹ Φ ( X ) ≈ Φ ( E [ X ]) + ϕ ( E [ X ]) ( X − E [ X ]) E [ Φ ( X )] ≈ Φ ( E [ X ]) + E [ ϕ ( E [ X ])] ( E [ X ] − E [ X ]) = E [ Φ ( X )] ⟹ Φ ( E [ W ( i ) − μ τ ] ) ≈ E [ Φ ( W ( i ) − μ τ ) ] = i n + 1 ⟹ E ( W ( i ) − μ τ ) ≈ Φ − 1 ( i n + 1 ) ≜ d n , i ( quantile of N ( 0 , 1 ) ) \begin{align*}
&\implies \Phi\left(E\left[\frac{W_{(i)}-\mu}{\tau}\right]\right)\approx E\left[\Phi\left(\frac{W_{(i)}-\mu}{\tau}\right)\right]=\frac{i}{n+1}\\
&\implies E\left(\frac{W_{(i)}-\mu}{\tau}\right)\approx\Phi^{-1}\left(\frac{i}{n+1}\right)\triangleq d_{n,i} (\text{quantile of }N(0,1))
\end{align*} ⟹ Φ ( E [ τ W ( i ) − μ ] ) ≈ E [ Φ ( τ W ( i ) − μ ) ] = n + 1 i ⟹ E ( τ W ( i ) − μ ) ≈ Φ − 1 ( n + 1 i ) ≜ d n , i ( quantile of N ( 0 , 1 )) Note that Φ ( d n , i ) = Φ ( Φ − 1 ( i n + i ) ) = i n + i ⟹ d n , 1 < d n , i < d n , n \Phi(d_{n,i})=\Phi(\Phi^{-1}(\frac{i}{n+i}))=\frac{i}{n+i}\implies d_{n,1}<d_{n,i}<d_{n,n} Φ ( d n , i ) = Φ ( Φ − 1 ( n + i i )) = n + i i ⟹ d n , 1 < d n , i < d n , n
⟺ E ( W ( i ) ) ≈ μ + τ ⋅ d n , i ⟺ W ( i ) ≈ μ + τ ⋅ d n , i + ε i ∗ with E ( ε i ∗ ) = 0 \begin{align*}
&\iff E(W_{(i)})\approx\mu+\tau\cdot d_{n,i}\\
&\iff W_{(i)}\approx\mu+\tau\cdot d_{n,i}+\varepsilon^*_i\text{ with } E(\varepsilon^*_i)=0
\end{align*} ⟺ E ( W ( i ) ) ≈ μ + τ ⋅ d n , i ⟺ W ( i ) ≈ μ + τ ⋅ d n , i + ε i ∗ with E ( ε i ∗ ) = 0 這看起來就像是一個簡單線性回歸模型,W ( i ) W_{(i)} W ( i ) d n , i d_{n,i} d n , i W ( i ) W_{(i)} W ( i ) d n , i d_{n,i} d n , i μ \mu μ τ \tau τ
Some research results:
E ( W ( i ) − μ τ ) ≈ Φ − 1 ( i − c n − 2 c + 1 ) ≜ d n , i c , ∀ c ∈ [ 0 , 1 ] E\left(\frac{W_{(i)}-\mu}{\tau}\right)\approx \Phi^{-1}\left(\frac{i-c}{n-2c+1}\right)\triangleq d_{n,i}^c,\quad \forall c \in [0,1] E ( τ W ( i ) − μ ) ≈ Φ − 1 ( n − 2 c + 1 i − c ) ≜ d n , i c , ∀ c ∈ [ 0 , 1 ] 因此,如果 h i i ≈ 0 h_{ii}\approx 0 h ii ≈ 0 n ≫ p n\gg p n ≫ p
⟹ e i ∼ : N ( 0 , σ 2 ) e i ∗ ∼ : N ( 0 , 1 ) γ i ∼ : N ( 0 , 1 ) \implies\begin{align*}
& e_i \simcolon N(0, \sigma^2)\\
& e^*_i \simcolon N(0, 1)\\
& \gamma_i \simcolon N(0, 1)
\end{align*} ⟹ e i ∼ : N ( 0 , σ 2 ) e i ∗ ∼ : N ( 0 , 1 ) γ i ∼ : N ( 0 , 1 ) i.e. 截距 μ = 0 \mu=0 μ = 0 τ = σ \tau=\sigma τ = σ e ( i ) e_{(i)} e ( i ) τ = 1 \tau=1 τ = 1 e ( i ) ∗ / γ ( i ) e^*_{(i)}/\gamma_{(i)} e ( i ) ∗ / γ ( i )
將 W ( i ) W_{(i)} W ( i ) d n , i d_{n,i} d n , i
因為 normal 分佈的 pdf 對於遠離中心的值很小,因此在 q-q plot 中,中心點的點會比較密集,而兩端的點會比較稀疏。因此我們會把看圖的重點放在兩端的部分。
不理想的圖會有兩種情況:
兩端趨近 0:代表數據 pdf 的兩端較薄,而中心較厚。
兩端遠離 0:代表數據 pdf 的兩端較厚,而中心較薄。
這種情況更糟,這代表更有可能出現更極端的值,甚至沒有期望值(e.g. Cauchy 分佈)。
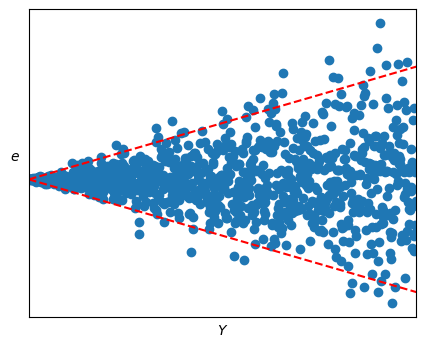
e i / e i ∗ / γ i e_i/e^*_i/\gamma_i e i / e i ∗ / γ i x ∗ x^* x ∗
這裡為了檢查是否還有其他重要的變數沒有加入到模型中。
如果殘差圖呈現一條在 x 軸附近的水平區帶,那麼這代表 x ∗ x^* x ∗
如果殘差圖呈現線性關係,那麼就將 x ∗ x^* x ∗
如果殘差圖呈現二次曲線關係,則將 x ∗ x^* x ∗ x ∗ 2 {x^*}^2 x ∗ 2
如果c殘差圖呈現波動範圍有明顯變化,那麼說明數據收集時可能有問題,比如資料的品質發生了變化。
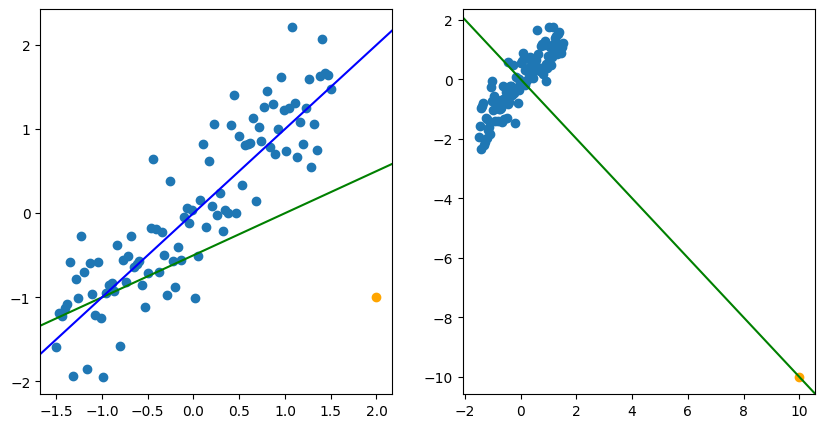
離群點
當畫原始點 Y Y Y x x x b ~ \utilde{b} b
有些會一定程度影響估計出的結果,而有些可能會讓估計呈現完全相反的結果。
Outlier : 與大部分數據有明顯差異的數據。會有不同的定義。
e.g. ∣ e i ∗ ∣ ≜ ∣ e i MSE ∣ > 4 ⟹ outlier \text{e.g. } |e^*_i|\triangleq\left|\frac{e_i}{\sqrt{\text{MSE}}}\right|>4\implies\text{outlier} e.g. ∣ e i ∗ ∣ ≜ MSE e i > 4 ⟹ outlier High-leverage point (influential): 是否包含這個數據會極大改變推論的結果。這個點的殘差可能會很小,因為回歸線會直接通過這個點。因為這個點可以撬動回歸線,所以這個點是高槓桿 的。 Remark: 直方圖、點圖或殘差圖可以幫我們找到 outliers,但可能無法找到 influential points。因此要用其他方法來找,比如:DBeta, DFitted, Cook's distance...
可以用以下方式找到 influential points:
h i i ∈ H h_{ii}\in H h ii ∈ H h i i > 2 p n h_{ii}>\frac{2p}{n} h ii > n 2 p i i i
Y ^ ~ = H Y ~ with H = ( h i j ) n × n , 0 ≤ h i i ≤ 1 , ∑ h i i = p ⟹ h i i ≈ p n \utilde{\hat{Y}}=H\utilde{Y}\quad\text{with }H=(h_{ij})_{n\times n},\quad 0\le h_{ii}\le 1,\quad\sum h_{ii}=p\implies h_{ii}\approx\frac{p}{n} Y ^ = H Y with H = ( h ij ) n × n , 0 ≤ h ii ≤ 1 , ∑ h ii = p ⟹ h ii ≈ n p ⟹ Y ^ i = ∑ j = 1 n h i j Y j = h i i Y i + ∑ j ≠ i h i j Y j \implies \hat{Y}_i=\sum_{j=1}^n h_{ij}Y_j=h_{ii}Y_i+\sum_{j\neq i}h_{ij}Y_j ⟹ Y ^ i = j = 1 ∑ n h ij Y j = h ii Y i + j = i ∑ h ij Y j i.e. h i i h_{ii} h ii Y i Y_i Y i Y ^ i \hat{Y}_i Y ^ i h i i h_{ii} h ii
如果 ∣ t i ∗ ∣ > t n − 1 − p , α 2 n |t^*_i|>t_{n-1-p,\frac{\alpha}{2n}} ∣ t i ∗ ∣ > t n − 1 − p , 2 n α i i i
因為 influential 是指有無這個點會有很大的影響。那麼我們先從原始資料 ( Y ~ , D ) (\utilde{Y}, D) ( Y , D ) i i i ( Y ~ ( i ) , D ( i ) ) (\utilde{Y}_{(i)}, D_{(i)}) ( Y ( i ) , D ( i ) ) i i i b ~ ( i ) \utilde{b}_{(i)} b ( i )
⟹ Y ^ ~ ( i ) = D b ~ ( i ) and e ~ ( i ) = Y ~ − Y ^ ~ ( i ) \implies \utilde{\hat{Y}}_{(i)}=D\utilde{b}_{(i)}\quad\text{and }\utilde{e}_{(i)}=\utilde{Y}-\utilde{\hat{Y}}_{(i)} ⟹ Y ^ ( i ) = D b ( i ) and e ( i ) = Y − Y ^ ( i ) 然後就能得到第 i i i Y ^ i ( i ) = ( D b ~ ( i ) ) i = c ~ i t b ~ ( i ) \hat{Y}_{i(i)}=(D\utilde{b}_{(i)})_i=\utilde{c}_i^t\utilde{b}_{(i)} Y ^ i ( i ) = ( D b ( i ) ) i = c i t b ( i ) c ~ i \utilde{c}_i c i i i i D D D
Def: d i = Y i − Y ^ i ( i ) d_i=Y_i-\hat{Y}_{i(i)} d i = Y i − Y ^ i ( i ) i i i
⟹ E ( d i ) = 0 E ( Y i ) = E ( Y ^ i ( i ) ) = c ~ i t β ~ σ 2 = σ 2 + σ 2 { Y ^ i ( i ) } Y i ⊥ Y i ( i ) = σ 2 + c ~ i t σ 2 { b ~ ( i ) } c ~ i = σ 2 + σ 2 ⋅ c ~ i t ( D t D ) − 1 c ~ i ⏟ ≜ A \begin{align*}
\implies &E(d_i)=0\qquad E(Y_i)=E(\hat{Y}_{i(i)})=\utilde{c}_i^t\utilde{\beta}\\
&\begin{align*}
\sigma^2&=\sigma^2+\sigma^2\set{\hat{Y}_{i(i)}}\quad Y_i\perp Y_{i(i)}\\
&=\sigma^2+\utilde{c}_i^t\sigma^2\set{\utilde{b}_{(i)}}\utilde{c}_i\\
&=\sigma^2+\sigma^2\cdot \underbrace{\utilde{c}_i^t(D^tD)^{-1}\utilde{c}_i}_{\triangleq A}
\end{align*}
\end{align*} ⟹ E ( d i ) = 0 E ( Y i ) = E ( Y ^ i ( i ) ) = c i t β σ 2 = σ 2 + σ 2 { Y ^ i ( i ) } Y i ⊥ Y i ( i ) �� = σ 2 + c i t σ 2 { b ( i ) } c i = σ 2 + σ 2 ⋅ ≜ A c i t ( D t D ) − 1 c i Also, MSE ( i ) = e ~ ( i ) t e ~ ( i ) n − 1 − p \text{MSE}_{(i)}=\frac{\utilde{e}^t_{(i)}\utilde{e}_{(i)}}{n-1-p} MSE ( i ) = n − 1 − p e ( i ) t e ( i ) S 2 d i = σ 2 { d i } ∣ σ 2 = MSE ( i ) = σ 2 { d i } ^ S^2{d_i}=\sigma^2\set{d_i}|_{\sigma^2=\text{MSE}_{(i)}}=\widehat{\sigma^2\set{d_i}} S 2 d i = σ 2 { d i } ∣ σ 2 = MSE ( i ) = σ 2 { d i }
⟹ t i ∗ = d i S { d i } ∼ t n − 1 − p \implies t_i^*=\frac{d_i}{S\set{d_i}}\sim t_{n-1-p} ⟹ t i ∗ = S { d i } d i ∼ t n − 1 − p 如果不希望做 n n n α → α n \alpha\to\frac{\alpha}{n} α → n α
Cook's distance
D i = ∑ ( Y ^ − Y ^ j ( i ) ) 2 p ⋅ MSE D_i=\frac{\sum(\hat{Y}-\hat{Y}_{j(i)})^2}{p\cdot\text{MSE}} D i = p ⋅ MSE ∑ ( Y ^ − Y ^ j ( i ) ) 2 代表 i i i Y ^ j ( i ) \hat{Y}_{j(i)} Y ^ j ( i ) D i D_i D i
⟹ i -th case has { major influence if D i > F p , n − p , 0.5 little apparent influence if D i > F p , n − p , 0.2 \implies i\text{-th case has}\begin{cases}
\text{major influence if } D_i>F_{p,n-p,0.5}\\
\text{little apparent influence if } D_i>F_{p,n-p,0.2}
\end{cases} ⟹ i -th case has { major influence if D i > F p , n − p , 0.5 little apparent influence if D i > F p , n − p , 0.2
Remark : 如果有 n n n t i ∗ , D i t_i^*,D_i t i ∗ , D i n + 1 n+1 n + 1 i i i
Fact : t i ∗ , D i t^*_i, D_i t i ∗ , D i ( Y ~ , D ) (\utilde{Y}, D) ( Y , D ) n + 1 n+1 n + 1
Q n × n = P n × n + U n × q V q × n ⟹ Q − 1 = P − 1 − P − 1 U ( I q + V P − 1 U ) − 1 V P − 1 \begin{align*}
& Q_{n\times n} = P_{n\times n} + U_{n\times q}V_{q\times n}\\
\implies & Q^{-1}=P^{-1}-P^{-1}U(I_q+V P^{-1}U)^{-1}V P^{-1}
\end{align*} ⟹ Q n × n = P n × n + U n × q V q × n Q − 1 = P − 1 − P − 1 U ( I q + V P − 1 U ) − 1 V P − 1 d i = e i 1 − h i i t i ∗ = e i n − p − 1 ( 1 − h i i SSE − e i 2 ) D i = e i 2 ⋅ h i i p ⋅ MSE ( 1 − h i i ) 2 \begin{align*}
& d_i=\frac{e_i}{1-h_{ii}}\\
& t^*_i=\frac{e_i\sqrt{n-p-1}}{\sqrt{(1-h_{ii}\text{SSE}-e_i^2)}}\\
& D_i=\frac{e_i^2\cdot h_{ii}}{p\cdot\text{MSE}(1-h_{ii})^2}
\end{align*} d i = 1 − h ii e i t i ∗ = ( 1 − h ii SSE − e i 2 ) e i n − p − 1 D i = p ⋅ MSE ( 1 − h ii ) 2 e i 2 ⋅ h ii Tests for Constancy of error Variance
當殘差圖呈現的波動沒有明顯變化或者明顯沒有變化時,我們會需要用一些檢驗來確認殘差的方差是否是常數。
Modified Levene test (Brown-Forsythe test)
適用於簡單線性回歸,並且方差隨著 X X X n ≫ p n\gg p n ≫ p e i e_i e i
Remark:在使用上,對於複回歸,我們也可以對每個解釋變數 x j x_j x j
假設有 n n n X X X n 1 n_1 n 1 n 2 n_2 n 2 n 1 + n 2 = n n_1+n_2=n n 1 + n 2 = n e i e_i e i e i 1 e_{i1} e i 1 e i 2 e_{i2} e i 2
令 e ~ j = median { e i j : i = 1 , ⋯ , n j } , j = 1 , 2 \tilde{e}_j=\text{median}\set{e_{ij}:i=1,\cdots,n_j}, j=1,2 e ~ j = median { e ij : i = 1 , ⋯ , n j } , j = 1 , 2
令 d i j = ∣ e i j − e j ~ ∣ , i = 1 , ⋯ , n j , j = 1 , 2 d_{ij}=|e_{ij}-\tilde{e_j}|, i=1,\cdots,n_j, j=1,2 d ij = ∣ e ij − e j ~ ∣ , i = 1 , ⋯ , n j , j = 1 , 2 d ˉ j = 1 n j ∑ i = 1 n j d i j \bar{d}_j=\frac{1}{n_j}\sum_{i=1}^{n_j}d_{ij} d ˉ j = n j 1 ∑ i = 1 n j d ij
把兩組 d i j d_{ij} d ij e i j e_{ij} e ij
t L ∗ ≜ d ˉ 1 − d ˉ 2 S 1 n 1 + 1 n 2 with S 2 = ∑ ( d i 1 − d ˉ 1 ) 2 + ∑ ( d i 2 − d ˉ 2 ) 2 n − 2 t^*_L\triangleq \frac{\bar{d}_1-\bar{d}_2}{S\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\qquad \text{with } S^2=\frac{\sum(d_{i1}-\bar{d}_1)^2+\sum(d_{i2}-\bar{d}_2)^2}{n-2} t L ∗ ≜ S n 1 1 + n 2 1 d ˉ 1 − d ˉ 2 with S 2 = n − 2 ∑ ( d i 1 − d ˉ 1 ) 2 + ∑ ( d i 2 − d ˉ 2 ) 2 在 H 0 : σ 2 { ε i } = σ 2 ∀ i H_0:\sigma^2\set{\varepsilon_i}=\sigma^2 \forall i H 0 : σ 2 { ε i } = σ 2 ∀ i d i 1 d_{i1} d i 1 d i 2 d_{i2} d i 2 n 1 , n 2 n_1,n_2 n 1 , n 2 t L ∗ ∼ t n − 2 t^*_L\sim t_{n-2} t L ∗ ∼ t n − 2
因此在 level α \alpha α ∣ t L ∗ ∣ > t n − 2 , α 2 |t^*_L|>t_{n-2,\frac{\alpha}{2}} ∣ t L ∗ ∣ > t n − 2 , 2 α H 0 H_0 H 0
Breusch-Pagan test
應用於樣本數足夠大,並且 ln σ i 2 = γ 0 + γ 1 x i \ln\sigma^2_i=\gamma_0+\gamma_1x_i ln σ i 2 = γ 0 + γ 1 x i X X X H 0 : σ 2 { ε i } = σ 2 H_0:\sigma^2\set{\varepsilon_i}=\sigma^2 H 0 : σ 2 { ε i } = σ 2 ∀ i ⟹ H 0 : γ 1 = 0 \forall i\implies H_0:\gamma_1=0 ∀ i ⟹ H 0 : γ 1 = 0
首先對於 e i 2 e^2_i e i 2 x i x_i x i SSR \text{SSR} SSR SSR ∗ \text{SSR}^* SSR ∗ Y Y Y x i x_i x i
X B P 2 ≜ SSR ∗ 2 ( SSE n ) 2 → n → ∞ χ 1 2 X^2_{BP}\triangleq\frac{\frac{\text{SSR}^*}{2}}{\left(\frac{\text{SSE}}{n}\right)^2}\xrightarrow{n\to\infty}\chi^2_1 X BP 2 ≜ ( n SSE ) 2 2 SSR ∗ n → ∞ χ 1 2 因此,當 X B P 2 > χ 1 , α 2 X^2_{BP}>\chi^2_{1,\alpha} X BP 2 > χ 1 , α 2 H 0 : σ 2 { ε i } = σ 2 ∀ i H_0:\sigma^2\set{\varepsilon_i}=\sigma^2\quad\forall i H 0 : σ 2 { ε i } = σ 2 ∀ i ≈ α \approx \alpha ≈ α
如果發生了方差不等的情況,我們可以有以下方法來調整:
在分析前先對 Y i Y_i Y i
Weighted LSE(WLSE)
Let E ( Y i ) = θ i E(Y_i)=\theta_i E ( Y i ) = θ i σ 2 { Y i } = σ 2 ( θ i ) \sigma^2\set{Y_i}=\sigma^2(\theta_i) σ 2 { Y i } = σ 2 ( θ i )
我們希望找到一個函數 f f f f ( Y i ) f(Y_i) f ( Y i )
Note:如果 f ′ ′ < ∞ f'' <\infty f ′′ < ∞ Y i Y_i Y i θ i \theta_i θ i θ i ∗ \theta^*_i θ i ∗
f ( Y i ) = f ( θ i ) + f ′ ( θ i ) ( Y i − θ i ) + 1 2 f ′ ′ ( θ i ∗ ) ( Y i − θ i ) 2 ⟺ f ( Y i ) − f ( θ i ) = f ′ ( θ i ) ( Y i − θ i ) + 1 2 f ′ ′ ( θ i ∗ ) ( Y i − θ i ) 2 \begin{align*}
f(Y_i)&=f(\theta_i)+f'(\theta_i)(Y_i-\theta_i)+\frac{1}{2}f''(\theta^*_i)(Y_i-\theta_i)^2\\
\iff f(Y_i)-f(\theta_i)&=f'(\theta_i)(Y_i-\theta_i)+\frac{1}{2}f''(\theta^*_i)(Y_i-\theta_i)^2
\end{align*} f ( Y i ) ⟺ f ( Y i ) − f ( θ i ) = f ( θ i ) + f ′ ( θ i ) ( Y i − θ i ) + 2 1 f ′′ ( θ i ∗ ) ( Y i − θ i ) 2 = f ′ ( θ i ) ( Y i − θ i ) + 2 1 f ′′ ( θ i ∗ ) ( Y i − θ i ) 2 當 ( Y i − θ i ) 2 ≈ 0 ⟹ E [ f ( Y i − θ i ) 2 ] ≈ 0 ⟹ E [ f ( Y i ) ] ≈ f ( θ i ) = f ( E [ Y i ] ) (Y_i-\theta_i)^2\approx 0\implies E[f(Y_i-\theta_i)^2]\approx 0\implies E[f(Y_i)]\approx f(\theta_i)=f(E[Y_i]) ( Y i − θ i ) 2 ≈ 0 ⟹ E [ f ( Y i − θ i ) 2 ] ≈ 0 ⟹ E [ f ( Y i )] ≈ f ( θ i ) = f ( E [ Y i ])
⟹ E [ ( f ( Y i ) − f ( θ i ) ) 2 ] ≈ σ 2 { f ( Y i ) } ≈ f ′ ( θ i ) 2 σ 2 { Y i } \implies E[(f(Y_i)-f(\theta_i))^2]\approx \sigma^2\set{f(Y_i)}\approx f'(\theta_i)^2\sigma^2\set{Y_i} ⟹ E [( f ( Y i ) − f ( θ i ) ) 2 ] ≈ σ 2 { f ( Y i ) } ≈ f ′ ( θ i ) 2 σ 2 { Y i }
i.e. σ 2 { f ( Y i ) } ≈ ( f ′ ( θ i ) ) 2 σ 2 { Y i } = ( f ′ ( θ i ) ) 2 σ 2 ( θ i ) = c 2 const in θ i i.e. f ′ ( θ i ) = c σ ( θ i ) \begin{align*}
&\text{i.e. }\sigma^2\set{f(Y_i)}\approx \left(f'(\theta_i)\right)^2\sigma^2\set{Y_i}=\left(f'(\theta_i)\right)^2\sigma^2(\theta_i)=c^2\text{ const in }\theta_i\\
&\text{i.e. }f'(\theta_i)=\frac{c}{\sigma(\theta_i)}
\end{align*}
i.e. σ 2 { f ( Y i ) } ≈ ( f ′ ( θ i ) ) 2 σ 2 { Y i } = ( f ′ ( θ i ) ) 2 σ 2 ( θ i ) = c 2 const in θ i i.e. f ′ ( θ i ) = σ ( θ i ) c A function f f f
f ′ ( θ i ) = c σ ( θ i ) f'(\theta_i)=\frac{c}{\sigma(\theta_i)} f ′ ( θ i ) = σ ( θ i ) c with constant c > 0 c>0 c > 0 variance-stabilizing transformation 方差穩定轉換。
Remark: δ \delta δ
n ( T n − θ ) → D N ( 0 , τ 2 ( θ ) ) ⟹ n ( g ( T n ) − g ( θ ) ) → D N ( 0 , ( g ′ ( θ ) ) 2 τ 2 ( θ ) ⏟ = c 2 ) \begin{align*}
&\sqrt{n}(T_n-\theta)\xrightarrow{D}N(0,\tau^2(\theta))\\
\implies& \sqrt{n}(g(T_n)-g(\theta))\xrightarrow{D}N(0,\underbrace{(g'(\theta))^2\tau^2(\theta)}_{=c^2})
\end{align*} ⟹ n ( T n − θ ) D N ( 0 , τ 2 ( θ )) n ( g ( T n ) − g ( θ )) D N ( 0 , = c 2 ( g ′ ( θ ) ) 2 τ 2 ( θ ) ) EX :
Y i ∼ P ( θ i ) Y_i\sim P(\theta_i) Y i ∼ P ( θ i ) E ( Y i ) = θ i = σ 2 { Y i } E(Y_i)=\theta_i=\sigma^2\set{Y_i} E ( Y i ) = θ i = σ 2 { Y i } σ 2 ( θ ) = σ 2 Y i = θ ⟹ σ ( θ ) = θ \sigma^2(\theta)=\sigma^2{Y_i}=\theta\implies\sigma(\theta)=\sqrt{\theta} σ 2 ( θ ) = σ 2 Y i = θ ⟹ σ ( θ ) = θ θ i \theta_i θ i
⟹ f ( t ) = ∫ 1 σ ( t ) d t = ∫ 1 t d t ∝ t ⟹ Y i → variance stablitice Y i ≜ Y i ∗ \begin{align*}
&\implies f(t)=\int \frac{1}{\sigma(t)} dt=\int \frac{1}{\sqrt{t}}dt\propto \sqrt{t}\\
&\implies Y_i\xrightarrow[\text{variance}]{\text{stablitice}} \sqrt{Y_i}\triangleq Y^*_i
\end{align*} ⟹ f ( t ) = ∫ σ ( t ) 1 d t = ∫ t 1 d t ∝ t ⟹ Y i stablitice variance Y i ≜ Y i ∗
Y i ∼ exp ( 1 θ ) Y_i\sim \exp(\frac{1}{\theta}) Y i ∼ exp ( θ 1 ) σ 2 ( θ ) = θ 2 \sigma^2(\theta)=\theta^2 σ 2 ( θ ) = θ 2 σ ( θ ) = θ \sigma(\theta)=\theta σ ( θ ) = θ
⟹ f ( t ) = ∫ 1 σ ( t ) d t = ∫ 1 t d t ∝ ln ( t ) \implies f(t)=\int \frac{1}{\sigma(t)} dt=\int \frac{1}{t}dt\propto \ln(t) ⟹ f ( t ) = ∫ σ ( t ) 1 d t = ∫ t 1 d t ∝ ln ( t )
σ 2 ( θ ) = θ 4 \sigma^2(\theta)=\theta^4 σ 2 ( θ ) = θ 4 σ ( θ ) = θ 2 \sigma(\theta)=\theta^2 σ ( θ ) = θ 2
⟹ f ( t ) = ∫ 1 σ ( t ) d t = ∫ 1 t 2 d t ∝ 1 t \implies f(t)=\int \frac{1}{\sigma(t)} dt=\int \frac{1}{t^2}dt\propto \frac{1}{t} ⟹ f ( t ) = ∫ σ ( t ) 1 d t = ∫ t 2 1 d t ∝ t 1
Y i ∼ Ber ( p ) Y_i\sim\text{Ber}(p) Y i ∼ Ber ( p ) σ 2 ( θ ) = θ ( 1 − θ ) \sigma^2(\theta)=\theta(1-\theta) σ 2 ( θ ) = θ ( 1 − θ ) σ ( θ ) = θ ( 1 − θ ) \sigma(\theta)=\sqrt{\theta(1-\theta)} σ ( θ ) = θ ( 1 − θ )
⟹ f ( t ) = ∫ 1 σ ( t ) d t = ∫ 1 t ( 1 − t ) d t ∝ arcsin ( t ) \implies f(t)=\int \frac{1}{\sigma(t)} dt=\int \frac{1}{\sqrt{t(1-t)}}dt\propto \arcsin(\sqrt{t}) ⟹ f ( t ) = ∫ σ ( t ) 1 d t = ∫ t ( 1 − t ) 1 d t ∝ arcsin ( t )
Most useful transformation in parctic :
σ ( θ ) \sigma(\theta) σ ( θ ) data's range transformation k θ k\theta k θ Y ≥ 0 Y\ge 0 Y ≥ 0 ln Y \ln Y ln Y k θ k\sqrt{\theta} k θ Y ≥ 0 Y\ge 0 Y ≥ 0 Y \sqrt{Y} Y θ 2 \theta^2 θ 2 Y ≥ 0 Y\ge 0 Y ≥ 0 1 Y \frac{1}{Y} Y 1 θ ( 1 − θ ) \sqrt{\theta(1-\theta)} θ ( 1 − θ ) 0 ≤ Y ≤ 1 0\le Y\le 1 0 ≤ Y ≤ 1 arcsin ( Y ) \arcsin(\sqrt{Y}) arcsin ( Y ) 1 − θ θ \frac{\sqrt{1-\theta}}{\theta} θ 1 − θ 0 ≤ Y ≤ 1 0\le Y\le 1 0 ≤ Y ≤ 1 1 − Y ( 1 − Y ) 3 2 3 \sqrt{1-Y}\frac{(1-Y)^\frac{3}{2}}{3} 1 − Y 3 ( 1 − Y ) 2 3 1 − θ 2 1-\theta^2 1 − θ 2 − 1 ≤ Y ≤ 1 -1\le Y\le 1 − 1 ≤ Y ≤ 1 ln ( 1 + Y 1 − Y ) \ln\left(\frac{1+Y}{1-Y}\right) ln ( 1 − Y 1 + Y )
但轉換可能會改變原本數據的分佈
Meta-theory
對方差進行穩定轉換,通常會讓數據看起來更像常態分佈。
因此如果發現方差不等的情況,要優先處理。
Weighted LSE
與原本的模型假設不同的是,我們假設方差並不是常數,即:
Y ~ = D β ~ + ε ~ where ε ~ ∼ N n ( 0 , ∑ ε ~ ) ∑ ε ~ = diag ( σ 1 2 , σ 2 2 , ⋯ , σ n 2 ) \utilde{Y}=D\utilde{\beta}+\utilde{\varepsilon}\quad\text{ where }\utilde{\varepsilon}\sim N_n(0,\bcancel{\sum}_{\utilde{\varepsilon}})\quad \bcancel{\sum}_{\utilde{\varepsilon}}=\text{diag}(\sigma^2_1,\sigma^2_2,\cdots,\sigma^2_n) Y = D β + ε where ε ∼ N n ( 0 , ∑ ε ) ∑ ε = diag ( σ 1 2 , σ 2 2 , ⋯ , σ n 2 ) 假設 σ i 2 = σ 2 c i 2 \sigma^2_i=\sigma^2c^2_i σ i 2 = σ 2 c i 2 c i > 0 c_i>0 c i > 0 c i c_i c i σ 2 \sigma^2 σ 2
Y i = β 0 + β 1 X i 1 + ⋯ + β k X i k + ε i ⟺ Y i c i = β 0 c i + β 1 c i X i 1 + ⋯ + β k c i X i k + ε i c i i.e. Y i c i = β 0 + β 1 X i 1 + ⋯ + β k X i k c i + ε i ∗ \begin{align*}
&Y_i=\beta_0+\beta_1X_{i1} + \cdots +\beta_kX_{ik}+\varepsilon_i\\
\iff& \frac{Y_i}{c_i}= \frac{\beta_0}{c_i}+\frac{\beta_1}{c_i}X_{i1} + \cdots +\frac{\beta_k}{c_i}X_{ik}+\frac{\varepsilon_i}{c_i}\\
\text{i.e. }& \frac{Y_i}{c_i}=\frac{\beta_0+\beta_1X_{i1} + \cdots +\beta_kX_{ik}}{c_i}+\varepsilon^*_i \tag{$*$}
\end{align*} ⟺ i.e. Y i = β 0 + β 1 X i 1 + ⋯ + β k X ik + ε i c i Y i = c i β 0 + c i β 1 X i 1 + ⋯ + c i β k X ik + c i ε i c i Y i = c i β 0 + β 1 X i 1 + ⋯ + β k X ik + ε i ∗ ( ∗ ) 其中 ε i ∗ ≜ ε i c i ∼ N ( 0 , c i ) \varepsilon^*_i\triangleq \frac{\varepsilon_i}{c_i}\sim N(0,c_i) ε i ∗ ≜ c i ε i ∼ N ( 0 , c i ) β ~ \utilde{\beta} β ( ∗ ) (*) ( ∗ )
Q W ( β ~ ) ≜ ∑ i = 1 n ( Y i c i − ( β 0 + β 1 X i 1 + ⋯ + β k X i k c i ) ) 2 = ∑ i = 1 n 1 c i 2 ( Y i − ( β 0 + β 1 X i 1 + ⋯ + β k X i k ) ) 2 = ( Y ~ − D β ~ ) t W ( Y ~ − D β ~ ) where W = diag { 1 c 1 2 , ⋯ , 1 c n 2 } = diag { w 1 , ⋯ , w n } \begin{align*}
Q_W(\utilde{\beta})&\triangleq \sum_{i=1}^n\left(\frac{Y_i}{c_i}-\left(\frac{\beta_0+\beta_1X_{i1} + \cdots +\beta_kX_{ik}}{c_i}\right) \right)^2\\
&=\sum_{i=1}^n\frac{1}{c_i^2}\left(Y_i-(\beta_0+\beta_1X_{i1} + \cdots +\beta_kX_{ik})\right)^2\\
&=(\utilde{Y}-D\utilde{\beta})^tW(\utilde{Y}-D\utilde{\beta})\quad\text{ where } W=\text{diag}\set{\frac{1}{c_1^2},\cdots,\frac{1}{c_n^2}}=\text{diag}\set{w_1,\cdots,w_n}
\end{align*} Q W ( β ) ≜ i = 1 ∑ n ( c i Y i − ( c i β 0 + β 1 X i 1 + ⋯ + β k X ik ) ) 2 = i = 1 ∑ n c i 2 1 ( Y i − ( β 0 + β 1 X i 1 + ⋯ + β k X ik ) ) 2 = ( Y − D β ) t W ( Y − D β ) where W = diag { c 1 2 1 , ⋯ , c n 2 1 } = diag { w 1 , ⋯ , w n } b ~ W \utilde{b}_W b W β \beta β Y ~ = D β ~ + ε ~ \utilde{Y}=D\utilde{\beta}+\utilde{\varepsilon} Y = D β + ε ε i = σ 2 c i 2 \varepsilon_i=\sigma^2c_i^2 ε i = σ 2 c i 2
Q W ( b ~ W ) = min β ~ Q W ( β ~ ) Q_W(\utilde{b}_W)=\min_{\utilde{\beta}}Q_W(\utilde{\beta}) Q W ( b W ) = β min Q W ( β ) 與 LSE 相似,Q W ( b ~ W ) = min β ~ Q W ( β ~ ) ⟺ b ~ W Q_W(\utilde{b}_W)=\min_{\utilde{\beta}}Q_W(\utilde{\beta})\iff \utilde{b}_W Q W ( b W ) = min β Q W ( β ) ⟺ b W D t W Y ~ = D t W D b ~ W D^tW\utilde{Y}=D^tWD\utilde{b}_W D t W Y = D t W D b W
如果 ( D t W D ) t (D^tWD)^t ( D t W D ) t b ~ W = ( D t W D ) − 1 D t W Y ~ \utilde{b}_W=(D^tWD)^{-1}D^tW\utilde{Y} b W = ( D t W D ) − 1 D t W Y
Note :
Q W ( β ) = ( Y ~ − D β ~ ) t W ( Y ~ − D β ~ ) = ( W 1 2 Y ~ − W 1 2 D β ~ ) t ( W 1 2 Y ~ − W 1 2 D β ~ ) where W 1 2 = diag { 1 c 1 , ⋯ , 1 c n } = ( Y ~ ∗ − D ∗ β ~ ) t ( Y ~ ∗ − D ∗ β ~ ) where Y ~ ∗ = W 1 2 Y ~ , D ∗ = W 1 2 D \begin{align*}
Q_W(\beta)&=(\utilde{Y}-D\utilde{\beta})^tW(\utilde{Y}-D\utilde{\beta})\\
&=(W^\frac{1}{2}\utilde{Y}-W^\frac{1}{2}D\utilde{\beta})^t(W^\frac{1}{2}\utilde{Y}-W^\frac{1}{2}D\utilde{\beta})\quad\text{where }W^\frac{1}{2}=\text{diag}\set{\frac{1}{c_1},\cdots,\frac{1}{c_n}}\\
&=(\utilde{Y}^*-D^*\utilde{\beta})^t(\utilde{Y}^*-D^*\utilde{\beta})\quad\text{where }\utilde{Y}^*=W^\frac{1}{2}\utilde{Y}, D^*=W^\frac{1}{2}D
\end{align*} Q W ( β ) = ( Y − D β ) t W ( Y − D β ) = ( W 2 1 Y − W 2 1 D β ) t ( W 2 1 Y − W 2 1 D β ) where W 2 1 = diag { c 1 1 , ⋯ , c n 1 } = ( Y ∗ − D ∗ β ) t ( Y ∗ − D ∗ β ) where Y ∗ = W 2 1 Y , D ∗ = W 2 1 D 這就想轉換成了一個新的模型 Y ~ ∗ = D ∗ β ~ + ε ~ ∗ \utilde{Y}^*=D^*\utilde{\beta}+\utilde{\varepsilon}^* Y ∗ = D ∗ β + ε ∗ ε i ∗ ∼ N ( 0 , σ 2 I n ) \varepsilon^*_i\sim N(0,\sigma^2I_n) ε i ∗ ∼ N ( 0 , σ 2 I n ) D ∗ D^* D ∗ ⟺ D \iff D ⟺ D
根據 Gauss-Markov theorem ,b ~ W \utilde{b}_W b W β ~ \utilde{\beta} β b ~ \utilde{b} b β ~ \utilde{\beta} β b ~ W \utilde{b}_W b W b ~ \utilde{b} b
在 ( D ∗ , Y ~ ∗ ) (D^*,\utilde{Y}^*) ( D ∗ , Y ∗ )
MSE W ≜ ( Y ~ ∗ − D ∗ b ~ W ) t ( Y ~ ∗ − D ∗ b ~ W ) n − p = ( Y ~ − D b ~ W ) t W ( Y ~ − D b ~ W ) n − p = e ~ t W e ~ n − p = 1 n − p ∑ i = 1 n e i 2 c i 2 \begin{align*}
\text{MSE}_W&\triangleq \frac{(\utilde{Y}^*-D^*\utilde{b}_W)^t(\utilde{Y}^*-D^*\utilde{b}_W)}{n-p}\\
&=\frac{(\utilde{Y}-D\utilde{b}_W)^tW(\utilde{Y}-D\utilde{b}_W)}{n-p}\\
&=\frac{\utilde{e}^tW\utilde{e}}{n-p}\\
&=\frac{1}{n-p}\sum_{i=1}^n\frac{e_i^2}{c_i^2}\\
\end{align*} MSE W ≜ n − p ( Y ∗ − D ∗ b W ) t ( Y ∗ − D ∗ b W ) = n − p ( Y − D b W ) t W ( Y − D b W ) = n − p e t W e = n − p 1 i = 1 ∑ n c i 2 e i 2 ⟹ S 2 { b ~ W } = MSE W ( D t W D ) − 1 \implies S^2\set{\utilde{b}_W}=\text{MSE}_W(D^tWD)^{-1} ⟹ S 2 { b W } = MSE W ( D t W D ) − 1 因此,如果 ε ~ ∼ N n ( 0 , σ 2 diag ( c 1 2 , ⋯ , c n 2 ) ) \utilde{\varepsilon}\sim N_n(0,\sigma^2\text{diag}(c^2_1,\cdots,c^2_n)) ε ∼ N n ( 0 , σ 2 diag ( c 1 2 , ⋯ , c n 2 )) σ 2 \sigma^2 σ 2 c i c_i c i b ~ W \utilde{b}_W b W β ~ \utilde{\beta} β
Y ^ ~ = D b ~ W \utilde{\hat{Y}}=D\utilde{b}_W Y ^ = D b W e ~ = Y ~ − Y ^ ~ \utilde{e}=\utilde{Y}-\utilde{\hat{Y}} e = Y − Y ^ MSE W = e ~ t W e ~ n − p \text{MSE}_W=\frac{\utilde{e}^tW\utilde{e}}{n-p} MSE W = n − p e t W e σ 2 \sigma^2 σ 2
如果我們對 σ i 2 \sigma^2_i σ i 2 σ i 2 \sigma^2_i σ i 2
做 Y ~ \utilde{Y} Y e ~ \utilde{e} e
通過 e i e_i e i σ i 2 \sigma^2_i σ i 2
當得到 σ 2 \sigma^2 σ 2 S 2 S^2 S 2 w i = 1 S i 2 w_i=\frac{1}{S^2_i} w i = S i 2 1
以下是一些估計方法的經驗總結:
如果 e e e X j X_j X j Y ∗ = ∣ e ∣ ∼ X j Y^*=|e|\sim X_{j} Y ∗ = ∣ e ∣ ∼ X j Y i ∗ ^ = S i \hat{Y_i^*}=S_i Y i ∗ ^ = S i
如果 e e e Y Y Y Y ∗ = ∣ e ∣ ∼ Y i Y^*=|e|\sim Y_i Y ∗ = ∣ e ∣ ∼ Y i Y i ∗ ^ = S i \hat{Y_i^*}=S_i Y i ∗ ^ = S i
如果 e 2 e^2 e 2 X j X_j X j Y ∗ = e 2 ∼ X j Y^*=e^2\sim X_{j} Y ∗ = e 2 ∼ X j Y i ∗ ^ = S i 2 \hat{Y_i^*}=S_i^2 Y i ∗ ^ = S i 2
如果 e e e X j X_j X j Y ∗ = ∣ e ∣ ∼ X j + X j 2 Y^*=|e|\sim X_j+X_j^2 Y ∗ = ∣ e ∣ ∼ X j + X j 2 Y i ∗ ^ = S i \hat{Y_i^*}=S_i Y i ∗ ^ = S i