跳至主要内容

線性模型

簡單線性模型（Simple Linear Regression, SLR）​

Definition

SLR i=1,⋯ ,n,Xi∈R1i=1,\cdots,n, X_i\in \R^1 and E[εi]=0E[\varepsilon_i]=0

Yi=β0+β1Xi+εiY_i=\beta_0+\beta_1X_i+\varepsilon_i

E[Yi∣X=Xi]=E[β0+β1Xi+εiE[Y_i|X=X_i]=E[\beta_0+\beta_1X_i+\varepsilon_i]=β0+β1Xi=f(Xi,β~)\beta_0+\beta_1X_i=f(X_i, \utilde{\beta}) 稱為回歸函數（regression function），其中 β~=(β0,β1)\utilde{\beta}=(\beta_0, \beta_1) 是未知參數。

複線性模型（Multiple Linear Model, MLR）​

複線性模型與 SLR 類似，但區別在於 Xi=(Xi,1,Xi,2,⋯ ,Xi,n)∈RnX_i=(X_{i,1},X_{i,2},\cdots,X_{i,n})\in \R^n 是多為向量。

Definition

MLR

i=1,⋯ ,nXn~∈Rk,k>1i=1,\cdots,n \utilde{X_n}\in \R^k, k>1

Yi=β0+β1Xi,1+β2Xi,2+⋯+βkXi,k+εiY_i=\beta_0+\beta_1X_{i,1}+\beta_2X_{i,2}+\cdots+\beta_kX_{i,k}+\varepsilon_i
Remark

  1. “線性”是指回歸函數 f(x;β~)f(x;\utilde{\beta}) 中的參數都是線性的。

  2. 在一些非線性關係中，通過將 XX 做一些變換，就也可以用線性模型來分析。

    e.g. Y=β0+β1sin⁡t+ε⇒x=sin⁡tY=β0+β1x+εY=\beta_0+\beta_1\sin t+\varepsilon \xRightarrow{x=\sin t} Y=\beta_0+\beta_1 x+\varepsilon

我們拿到一組數據 (X1,Y1),⋯ ,(Xn,Yn)(X_1,Y_1),\cdots,(X_n,Y_n)，我們假設這組數據是由一個線性模型產生的，即 Yi=β0+βXi+εiY_i=\beta_0+\beta X_i+\varepsilon_i，但我們不知道 β~\utilde{\beta}，並且 εi\varepsilon_i 是一個隨機變量。

我們的目標是通過這組數據來估計 β~\utilde{\beta}，得到 β~^\hat{\utilde{\beta}}，然后通過 β~^\hat{\utilde{\beta}} 來得到预测值 Yi^=f(Xi;β~^)\hat{Y_i}=f(X_i;\hat{\utilde{\beta}})。

最小二乘估計（Least Squares Estimation, LSE）​

Definition

残差（residual）：ei=Yi−Yi^e_i=Y_i-\hat{Y_i}

我們希望預測值 Yi^\hat{Y_i} 與實際值 YiY_i 的差距越小越好，即 ∑i=1nei2=∑i=1n(Yi−Yi^)2\sum_{i=1}^n e_i^2=\sum_{i=1}^n(Y_i-\hat{Y_i})^2 越小越好。為此，我們通常會使用 最小二乘估計（Least Squares Estimation, LSE）。

Definition

對於線性回歸 Yi=f(Xi;β~)+εiY_i=f(X_i;\utilde{\beta})+\varepsilon_i，定義：

Q(β~)=∑i=1n(Yi−E[Yi])2=∑i=1n(Yi−f(Xi;β~))2Q(\utilde{\beta})=\sum_{i=1}^n(Y_i-E[Y_i])^2=\sum_{i=1}^n(Y_i-f(X_i;\utilde{\beta}))^2

稱 bb 是 β~\utilde{\beta} 的 LSE   ⟺  Q(b)=min⁡β~Q(β~)\iff Q(b)=\min_{\utilde{\beta}} Q(\utilde{\beta})

Theorem
b0=Yˉ−b1Xˉb1=∑i=1n(Xi−Xˉ)(Yi−Yˉ)∑i=1n(Xi−Xˉ)2=∑i=1nXi(Yi−Yˉ)∑i=1n(Xi−Xˉ)2=∑i=1n(Xi−Xˉ)Yi∑i=1n(Xi−Xˉ)2\begin{align*} b_0&= \bar{Y}-b_1\bar{X} \\ b_1&= \frac{\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=1}^n(X_i-\bar{X})^2}= \frac{\sum_{i=1}^nX_i(Y_i-\bar{Y})}{\sum_{i=1}^n(X_i-\bar{X})^2}= \frac{\sum_{i=1}^n(X_i-\bar{X})Y_i}{\sum_{i=1}^n(X_i-\bar{X})^2} \end{align*}

  ⟹  Yi^=b0+b1Xi=Yˉ−b1Xˉ+b1Xi=Yˉ+b1(Xi−Xˉ)\implies \hat{Y_i}=b_0+b_1X_i=\bar{Y}-b_1\bar{X}+b_1X_i=\bar{Y}+b_1(X_i-\bar{X})。

  ⟹  ei=Yi−Yiˉ=Yi−Yˉ−b1(Xi−Xˉ)\implies e_i=Y_i-\bar{Y_i}=Y_i-\bar{Y}-b_1(X_i-\bar{X})

  1. ∑i=1nei=∑(Yi−Yˉ−b1(Xi−Xˉ))=∑(Yi−Yˉ)−b1∑(Xi−Xˉ)=0\sum_{i=1}^n e_i=\sum(Y_i-\bar{Y}-b_1(X_i-\bar{X}))=\sum(Y_i-\bar{Y})-b_1\sum(X_i-\bar{X})=0

  2. ∑i=1nYi^=∑(Yˉ−b1(Xi−Xˉ))=nYˉ−b1∑(Xi−Xˉ)\sum_{i=1}^n \hat{Y_i}=\sum(\bar{Y}-b_1(X_i-\bar{X}))=n\bar{Y}-b_1\sum(X_i-\bar{X})

      ⟹  1n∑i=1nYi^=Yˉ\implies \frac{1}{n}\sum_{i=1}^n \hat{Y_i}=\bar{Y}, i.e. 預測值的中心點是數據值的中心點。

∑i=1n(Xiei)=∑i=1n[Xi(Yi−Yˉ−b1(Xi−Xˉ))]=∑i=1nXi(Yi−Yˉ)−b1∑i=1nXi(Xi−Xˉ)=∑i=1nXi(Yi−Yˉ)−∑i=1nXi(Yi−Yˉ)∑i=1n(Xi−Xˉ)2∑i=1n(Xi−Xˉ)2∵∑i=1nXi(Xi−Xˉ)=∑i=1n(Xi−Xˉ)2=0\begin{align*} \sum_{i=1}^n(X_ie_i)&=\sum_{i=1}^n [X_i(Y_i-\bar{Y}-b_1(X_i-\bar{X}))] \\ &=\sum_{i=1}^n X_i(Y_i-\bar{Y})-b_1\sum_{i=1}^n X_i(X_i-\bar{X}) \\ &=\sum_{i=1}^n X_i(Y_i-\bar{Y})- \frac{\sum_{i=1}^nX_i(Y_i-\bar{Y})}{\sum_{i=1}^n(X_i-\bar{X})^2} \sum_{i=1}^n (X_i-\bar{X})^2 \quad \because\sum_{i=1}^n X_i(X_i-\bar{X})=\sum_{i=1}^n (X_i-\bar{X})^2\\ &=0 \end{align*}

將 X~\utilde{X} 和 e~\utilde{e} 寫成向量，i.e. X~=(X1,⋯ ,Xn)t∈Rn,e~=(e1,⋯ ,en)t∈Rn\utilde{X}=(X_1,\cdots,X_n)^t\in \R^n, \utilde{e}=(e_1,\cdots,e_n)^t\in \R^n，則 X~te~=0  ⟹  X~⊥e~\utilde{X}^t\utilde{e}=0 \implies \utilde{X} \perp \utilde{e} （垂直）。

  1. ∑i=1nYi^ei=∑i=1nb0ei+b1∑i=1nXiei=0+0\sum_{i=1}^n\hat{Y_i}e_i=\sum_{i=1}^n b_0e_i+b_1\sum_{i=1}^nX_ie_i=0+0, let Y^~=(Y1^,⋯ ,Yn^)t∈Rn\utilde{\hat{Y}}=(\hat{Y_1},\cdots,\hat{Y_n})^t\in \R^n

      ⟹  Y^~te~=0\implies \utilde{\hat{Y}}^t\utilde{e}=0, i.e. Y^~⊥e~\utilde{\hat{Y}}\perp \utilde{e}

    since e~=Y~−Y^~  ⟹  Y^~⊥Y~−Y^~\utilde{e}=\utilde{Y}-\utilde{\hat{Y}}\implies\utilde{\hat{Y}}\perp\utilde{Y}-\utilde{\hat{Y}}

    alt text

    所以預測值 Yi^~\utilde{\hat{Y_i}} 是 Y~\utilde{Y} 的投影。

  2. 擬合的回歸函數 Yi^=Yˉ+b1(Xi−Xˉ)\hat{Y_i}=\bar{Y}+b_1(X_i-\bar{X}) 通過點 (Xˉ,Yˉ)(\bar{X},\bar{Y})。

最佳線性不偏預測（Best Linear Unbiased Estimator, BLUE）​

Q: 最小二乘法總是能得到一個好的 β^~\utilde{\hat{\beta}} 嗎？或者說，在什麼情況下最小二乘法難以得到一個好的 β~\utilde{\beta}？

  1. 在下圖情況中，如果我們計算殘差 eie_i，雖然可能會得到和為 0 的結果，但殘差的分佈有很明顯的正負聚集現象。而我們希望殘差的正負隨機分佈的。

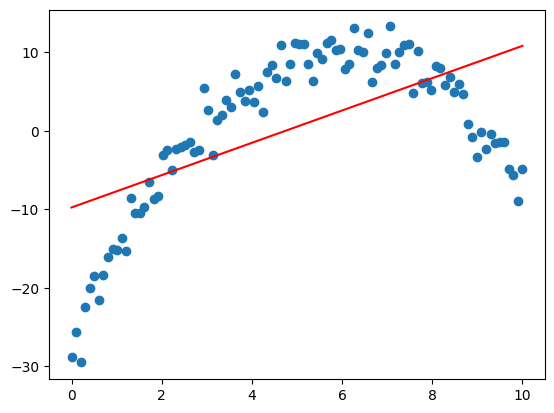
    alt text

    為了避免這種情況，我們需要誤差的期望為 0，即 E[ε~]=0E[\utilde{\varepsilon}]=0。

  2. 下圖中的數據，隨著 XX 的增加，數據也越分散。

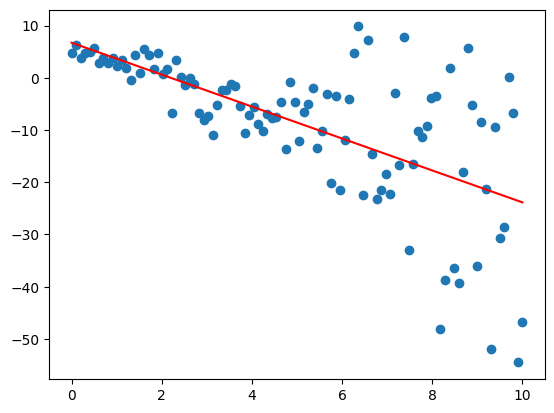
    alt text

    為了避免這種情況，我們需要所有誤差的方差是一樣的，即 Var[e~]=σ2Var[\utilde{e}]=\sigma^2，其中 σ2\sigma^2 是一個常數。

  3. 當沒有按照正規的程序獲取數據時，可能會出現下圖的情況。各個數據之間可能存在著相互關聯的情況。那麼擬合出來的回歸線會存在誤導性。

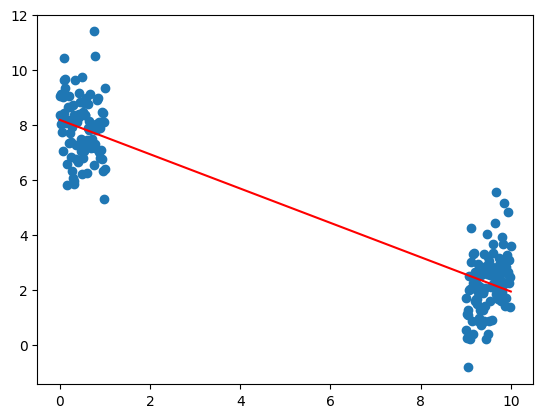
    alt text

    為了避免這種情況，我們需要所有誤差之間是沒有線性關係的，即 Cov[ei,ej]=0,∀i≠jCov[e_i, e_j]=0, \forall i\neq j。

Definition

formal statement of the of linear regression model

Yi=f(Xi~;β~)+εi=β0+β1Xi,1+⋯+βkXi,k+εi\begin{align*} Y_i&=f(\utilde{X_i}; \utilde{\beta})+\varepsilon_i \\ &=\beta_0+\beta_1 X_{i,1}+\cdots+\beta_k X_{i,k}+\varepsilon_i \\ \end{align*}

with the following conditions:

  1. E[εi]=0E[\varepsilon_i]=0
  2. Var[εi]=σ2{ εi }=σ2Var[\varepsilon_i]=\sigma^2\set{\varepsilon_i}=\sigma^2
  3. Cov[εi,εj]=σ{ εi,εj }=0Cov[\varepsilon_i,\varepsilon_j]=\sigma\set{\varepsilon_i,\varepsilon_j}=0

我們可以直接得到結論：

  1. E[Yi]=f(Xi~,β~)E[Y_i]=f(\utilde{X_i},\utilde{\beta}) 是回歸函數。
  2. σ2{ Yi }=σ2{ εi }=σ2\sigma^2\set{Y_i}=\sigma^2\set{\varepsilon_i}=\sigma^2，因為 f(Xi~,β~)f(\utilde{X_i},\utilde{\beta}) 是一個常數。
  3. σ{ Yi,Yj }=σ{ εi,εj }=0\sigma\set{Y_i,Y_j}=\sigma\set{\varepsilon_i,\varepsilon_j}=0.

Recall 對於 SLR，當我們已經拿到數據 X~\utilde{X}，β0,β1\beta_0, \beta_1 的 LSE 是:

b0=Yˉ−b1Xˉ,b1=∑i=1n(Xi−Xˉ)(Yi−Yˉ)∑i=1n(Xi−Xˉ)2b_0=\bar{Y}-b_1\bar{X}, \qquad b_1=\frac{\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=1}^n(X_i-\bar{X})^2}   ⟹  E[b1]=∑(Xi−Xˉ)EYi∑(Xi−Xˉ)2=∑(Xi−Xˉ)(β0+β1Xi)∑(Xi−Xˉ)2=β1E[b0]=E[Yˉ−b1Xˉ]=EYˉ−XˉE[b1]=β0+β1Xˉ−Xˉβ1=β0\begin{align*} \implies & E[b_1] = \frac{\sum(X_i-\bar{X})EY_i}{\sum(X_i-\bar{X})^2}=\frac{\sum(X_i-\bar{X})(\beta_0+\beta_1 X_i)}{\sum(X_i-\bar{X})^2}=\beta_1 \\ & E[b_0]=E[\bar{Y}-b_1\bar{X}]=E\bar{Y}-\bar{X}E[b_1]=\beta_0+\beta_1\bar{X}-\bar{X}\beta_1=\beta_0 \end{align*}

  ⟹  EYi^=E[b0+b1Xi]=β0+β1Xi=EYi\implies E\hat{Y_i}=E[b_0+b_1X_i]=\beta_0+\beta_1X_i=EY_i，因此 Yi^\hat{Y_i} 是 YiY_i 的無偏估計。

  ⟹  E[ei]≜E[Yi−Yi^]=0\implies E[e_i]\triangleq E[Y_i-\hat{Y_i}]=0

Definition

∑wiYi\sum w_iY_i 被稱為線性估計量（linear estimator）。

b1=∑(Xi−Xˉ)Yi∑(Xi−Xˉ)2=∑kiYi,with ki=Xi−Xˉ∑(Xi−Xˉ)2 and ∑ki=0b0=Yˉ−b1Xˉ=∑(1n−kiXˉ)Yi=∑ciYi,with ci=1n−kiXˉ and ∑ci=1\begin{align*} &b_1 = \frac{\sum(X_i-\bar{X})Y_i}{\sum(X_i-\bar{X})^2}=\sum k_iY_i, \quad \text{with }k_i=\frac{X_i-\bar{X}}{\sum(X_i-\bar{X})^2} \text{ and } \sum k_i=0 \\ &b_0 = \bar{Y}-b_1\bar{X}=\sum(\frac{1}{n}-k_i\bar{X})Y_i=\sum c_iY_i, \quad \text{with }c_i=\frac{1}{n}-k_i\bar{X} \text{ and } \sum c_i=1 \end{align*}

因此 b0,b1b_0,b_1 是 β0,β1\beta_0,\beta_1 的線性無偏估計。

Remark

Same for MLR

Theorem

Gauss-Markov theorem

When E(εi)=0,σ2{ εi }=0,σ{ εi,εj }=0E(\varepsilon_i)=0, \sigma^2\set{\varepsilon_i}=0, \sigma\set{\varepsilon_i,\varepsilon_j}=0

Then b~\utilde{b} are the Best Linear Unbiased Estimators (BLUE) of β~\utilde{\beta}.

σ2{ b1 }=σ2{ ∑kiYi }=∑ki2σ2{ Yi }+∑i≠jkikjσ{ Yi,Yj }=σ2∑ki2since σ2{ Yi }=σ2,σ{ Yi,Yj }=0=σ2∑(Xi−Xˉ)2(∑(Xi−Xˉ)2)2=σ2∑(Xi−Xˉ)2  ⟹  數據越分散越好σ2{ b0 }=σ2{ ∑ciYi }=∑ci2σ2{ Yi }+∑i≠jcicjσ{ Yi,Yj }=σ2∑ci2since σ2{ Yi }=σ2,σ{ Yi,Yj }=0=σ2∑(1n2−2Xkiˉn+ki2Xˉ2)=σ2(1n+Xˉ2∑(Xi−Xˉ)2)since ∑ki=0  ⟹  數據越多越好，並且希望使Xˉ=0\begin{align*} \sigma^2\set{b_1}&=\sigma^2\set{\sum k_iY_i}\\ &=\sum k_i^2\sigma^2\set{Y_i}+\sum_{i\neq j}k_ik_j\sigma\set{Y_i,Y_j}\\ &=\sigma^2\sum k_i^2 \quad \text{since }\sigma^2\set{Y_i}=\sigma^2, \sigma\set{Y_i,Y_j}=0\\ &=\sigma^2 \frac{\sum(X_i-\bar{X})^2}{(\sum(X_i-\bar{X})^2)^2}=\frac{\sigma^2}{\sum(X_i-\bar{X})^2}\\ &\implies \text{數據越分散越好}\\ \sigma^2\set{b_0}&=\sigma^2\set{\sum c_iY_i}\\ &=\sum c_i^2\sigma^2\set{Y_i}+\sum_{i\neq j}c_ic_j\sigma\set{Y_i,Y_j}\\ &=\sigma^2\sum c_i^2 \quad \text{since }\sigma^2\set{Y_i}=\sigma^2, \sigma\set{Y_i,Y_j}=0\\ &=\sigma^2 \sum (\frac{1}{n^2}-2\frac{\bar{Xk_i}}{n}+k_i^2\bar{X}^2)\\ &=\sigma^2 (\frac{1}{n}+\frac{\bar{X}^2}{\sum(X_i-\bar{X})^2}) \quad \text{since }\sum k_i=0\\ &\implies \text{數據越多越好，並且希望使} \bar{X}=0 \end{align*}

變異數分析（Analysis of Variance, ANOVA）​

我們想要知道目標 Y~\utilde{Y} 的變化量能否被預測值解釋。而变异数分析是在计算数据与均值之间的差异。

Note:

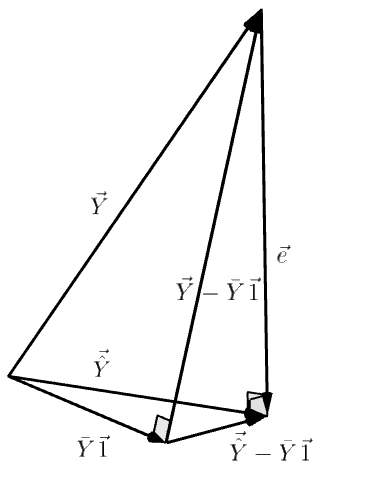
alt text

Yˉ~⊥e~=Y~−Yˉ~  ⟹  ∣∣Y~∣∣2=∣∣Yˉ~∣∣2+∣∣e~∣∣2\utilde{\bar{Y}}\perp \utilde{e}=\utilde{Y}-\utilde{\bar{Y}} \implies ||\utilde{Y}||^2=||\utilde{\bar{Y}}||^2+||\utilde{e}||^2

∑ei=0  ⟹  e~⋅1~=0  ⟹  e~⊥1~\sum e_i=0\implies \utilde{e}\cdot \utilde{1}=0 \implies \utilde{e}\perp \utilde{1}

  ⟹  ∑[e⋅(Yi^−Yˉ)]=∑eiYi^+Yˉ∑ei⋅1=0  ⟹  e~⊥Y^~−Yˉ1~\implies \sum[e\cdot(\hat{Y_i}-\bar{Y})]=\sum e_i\hat{Y_i} + \bar{Y}\sum e_i\cdot 1 = 0 \implies \utilde{e}\perp \utilde{\hat{Y}}-\bar{Y}\utilde{1}

  ⟹  ∣∣Y~−Yˉ1~∣∣2=∣∣Y^~−Yˉ1~∣∣2+∣∣e~∣∣2\implies ||\utilde{Y}-\bar{Y}\utilde{1}||^2=||\utilde{\hat{Y}}-\bar{Y}\utilde{1}||^2+||\utilde{e}||^2

i.e.∑(Yi−Yˉ)2⏟SSTO=∑(Yi^−Yˉ)2⏟SSR+∑(Y−Yi^)2⏟SSE\text{i.e.}\quad \underbrace{\sum(Y_i-\bar{Y})^2}_{\text{SSTO}}=\underbrace{\sum(\hat{Y_i}-\bar{Y})^2}_{\text{SSR}}+\underbrace{\sum(Y-\hat{Y_i})^2}_{\text{SSE}}
Definition
SSTO=∑(Yi−Yˉ)2Sum of Squared Total var (Of Y)SSR=∑(Yi^−Yˉ)2Regression Sum of SquaresSSE=∑(Y−Yi^)2Error Sum of Squares\begin{align*} \text{SSTO}&=\sum(Y_i-\bar{Y})^2 \quad \text{Sum of Squared Total var (Of Y)} \\ \text{SSR}&=\sum(\hat{Y_i}-\bar{Y})^2 \quad \text{Regression Sum of Squares} \\ \text{SSE}&=\sum(Y-\hat{Y_i})^2 \quad \text{Error Sum of Squares} \end{align*}
  • SSTO：表示數據 YY 與其均值 Yˉ\bar{Y} 之間的差異，也就是數據的變異量。
  • SSR：表示預測值 Y^\hat{Y} 與均值 Yˉ\bar{Y} 之間的差異。代表了模型解釋的變異量。SSR 越大，說明模型解釋的變異量越多。
  • SSE：殘差的平方和。代表了模型無法解釋的變異量。SSE 越小，說明模型無法解釋的變異量越少。
Theorem

Fundamental identity

dfSSTO=SSR+SSESLRn−1=1+n−2MLRn−1=k+n−(k+1)⏟p=參數量\begin{alignat*}{4} \text{df} \quad& \text{SSTO}&\quad=&\quad\text{SSR}&+\quad&\text{SSE}\\ \text{SLR} \quad&n-1&\quad=&\quad 1 &+ \quad&n-2\\ \text{MLR} \quad&n-1&\quad=&\quad k &+ \quad&n-\underbrace{(k+1)}_{p= \text{參數量}} \end{alignat*}
  • df: 自由度（degree of freedom）
  • k: 自變量的個數
E[SSE]=E[∑ei2]=∑E[ei2]=E[ei]=0∑σ2{ ei }=(n−p)σ2E[SSE]=E[\sum e_i^2]=\sum E[e_i^2]\xlongequal{E[e_i]=0} \sum \sigma^2\set{e_i}=(n-p)\sigma^2   ⟹  E[SSEn−p]=σ2\implies E[\frac{SSE}{n-p}]=\sigma^2
Definition
MSE≜SSEn−pMSR≜SSRkMSE\triangleq\frac{SSE}{n-p}\qquad MSR\triangleq\frac{SSR}{k}

Hence, MSE is unbiased for σ2\sigma^2.

Remark

在回歸中，我們通常使用 MSE 估計 σ2\sigma^2。而 σ\sigma 則用 MSE\sqrt{\text{MSE}} 估計。

Definition

對於 σ2{ ∗ }=σ2⋅c\sigma^2\set{*}=\sigma^2\cdot c，我們定義一個估計方法：

S2{ ∗ }=MSE⋅c=σ2^{ ∗ }S^2\set{*}=MSE\cdot c = \hat{\sigma^2}\set{*}

E.g.

σ2{ b1 }=σ21∑(Xi−Xˉ)2  ⟹  S2{ b1 }=MSE1∑(Xi−Xˉ)2\sigma^2\set{b_1}= \sigma^2\frac{1}{\sum(X_i-\bar{X})^2}\implies S^2\set{b_1}= MSE\frac{1}{\sum(X_i-\bar{X})^2}

因此 S2∗σ2{ ∗ }\frac{S^2{*}}{\sigma^2\set{*}} 的比值永遠會是 MSEσ2\frac{MSE}{\sigma^2}。

常態誤差回歸模型（Normal Error Regression Model）​

在回歸模型的基礎上，我們進一步假設誤差項 εi\varepsilon_i 是服從常態分佈的。

Definition
Yi=f(Xi~;β~)+εi,εi∼iidN(0,σ2)Y_i=f(\utilde{X_i};\utilde{\beta})+\varepsilon_i, \quad \varepsilon_i\overset{\text{iid}}{\sim} N(0,\sigma^2)

因此 YiY_i 也會獨立服從 N(f(Xi~;β~),σ2)N(f(\utilde{X_i};\utilde{\beta}),\sigma^2)。既然 YiY_i 的分佈是已知的，我們就可以構建它的似然函數。

L(β~,σ2)=∏i=1n12πσ2exp⁡(−(Yi−f(Xi~;β~))22σ2)=1(2πσ2)n/2exp⁡(−12σ2∑i=1n(Yi−f(Xi~;β~))2)=1(2πσ2)n/2exp⁡(−12σ2∑i=1n(Yi−Yi^))2)=1(2πσ2)n/2exp⁡(−12σ2Q(β~))\begin{align*} L(\utilde{\beta},\sigma^2)&=\prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(Y_i-f(\utilde{X_i};\utilde{\beta}))^2}{2\sigma^2}\right)\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n(Y_i-f(\utilde{X_i};\utilde{\beta}))^2\right)\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n(Y_i-\hat{Y_i}))^2\right)\\ &=\frac{1}{(2\pi\sigma^2)^{n/2}}\exp\left(-\frac{1}{2\sigma^2}Q(\utilde{\beta})\right) \end{align*}

  ⟹  \implies 在 SLR 中，β0^MLE=b0,β1^MLE=b1\hat{\beta_0}_{MLE} = b_0, \hat{\beta_1}_{MLE} = b_1。並且

σ2^MLE=1n∑i=1n(Yi−Yi^)2=SSEn\hat{\sigma^2}_{MLE}=\frac{1}{n}\sum_{i=1}^n(Y_i-\hat{Y_i})^2=\frac{SSE}{n}