這裡,我們使用常態誤差歸回模型來進行相關性分析。
Yi=β0+β1Xi+εi
估計量的分佈
之前我們已經證明了 b0,b1 是線性的,也就是可以表達為:
b1=∑kiYiwith ki=∑(Xi−Xˉ)2Xi−Xˉ
b0=∑ciYiwith ci=n1−kiXˉ
因為 ki 是 Xi 的函數,而 Xi 是固定的,所以 ki 和 ci 是常數。因此 b0,b1 是 Yi 的線性組合。因為 Yidεi∼iidN(0,σ2),所以 b0,b1 也是常態分佈。
b1∼N(E[b1],σ2[b1])dN(β1,σ2{b1})with σ2{b1}=∑(Xi−Xˉ)2σ2b0∼N(E[b0],σ2[b0])dN(β0,σ2{b0})with σ2{b0}=σ2(n1+∑(Xi−Xˉ)2Xˉ2)
⟹σ{bi}bi−βi∼N(0,1)with σ{bi}=σ2{bi}
σ{wtY,dtY}⟺=σ2⋅wtd=0wtd=0,w,d are linearly independent 這可以證明
SSE⊥b0,b1
σ2SSE∼χn−p2SLPχn−22 之前我們說 (bj−βj)/σ{bj} 是標準常態分佈。但在實際應用中,我們並不知道 σ2,所以我們應該要用 SSE 來估計 σ2。
S{bi}bi−βj=σ{bi}bi−βi/σ2{bi}S2{bi}=σ2MSE=σ{bi}bi−βi/(n−p)σ2SSEnote σ2SSE∼χn−p2=dχn−p2/(n−p)N(0,1)∼tn−p分子分母獨立
⟹S{bi}bi−βi∼tn−pSLRtn−2
信賴區間
之前我們計算的是在得到數據後,β 最有可能的值。但單點估計大概率不會是真實值。因此我們還會關注 β 會落在什麼範圍裡。
Def tm,α0 s.t. P(tm>tm,α0)=α0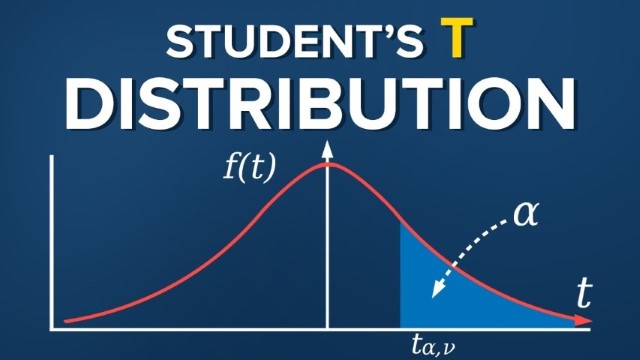
在上面的定義中,我們只是計算可以讓右端的面積是 α0 的點。我們還可以考慮左右兩端的面積加起來會是 α0 的兩個點。
⟹P(S{bi}bi−βi≤tn−p,2α)=1−α0
⟹P(bi−S{bi}tn−p,2α≤βi≤bi+S{bi}tn−p,2α)=1−α0
⟹P(βi∈[bi±S{bi}tn−p,2α])=1−α0
CI(β;α)=[bi±S{bi}tn−p,2α]被稱爲 βi 的 100(1−α)% 信賴區間(Confidence Interval),i.e. 我們有 100(1−α)% 的信心認為 βi 落在這個區間��裡。
Fact:
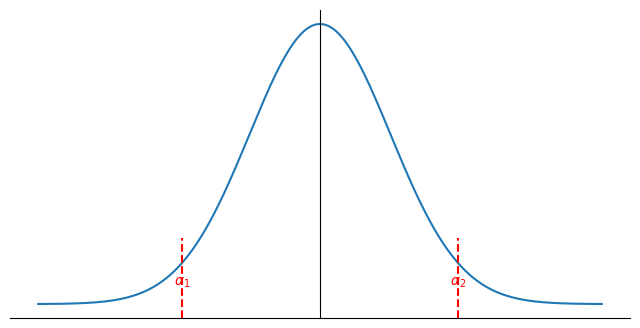
在任何滿足 α1+α2=α0 的組合中,α1=2α0=α2 會是最好的。⟹CI(β;α) 是 UMAU 1−α 信賴區間。
假設檢定
一般來說,當我們做假設檢定 H0:βi=βi,0 vs H1:βi=βi,0 時
在顯著水平(Significance Level) α 下,我們會拒絕 H0 ⟺βj,0∈/CI(βi;α)=[bi±S{bi}tn−p,2α]
i.e.
S{bi}bi−βi,0>tn−p,2α
而如果 ∣S{bi}bi−βi,0∣<tn−p,2α,就代表數據沒有提供足夠的證據拒絕 H0。
顯著水平其實就是 H0 被錯誤拒絕的機率,i.e. α=P(rej H0∣H0 is true)。
當我們想要知道 X 和 Y 是否有顯著的線性關係時,我們會做假設檢定 H0:β1=0 vs H1:β1=0。
t∗≜S{b1}b1∼tn−2H0:β1=0
根據已經得到的數據計算 t∗=t0∗
- 如果 ∣t0∗∣>tn−2,2α⟺ 拒絕 H0,i.e. X 和 Y 在 sig. level α 下有顯著的線性關係。
- 如果 ∣t0∗∣≤tn−2,2α⟺ 不拒絕 H0,i.e.沒有足夠的證據認為 X 和 Y 有顯著的線性關係。
P-value
在判斷是否拒絕 H0 前,我們需要先確定顯著水平 α 才能查表得到 tn−2,2α。
注意到 ∣t0∗∣>tn−2,2α 代表 pdf 曲線下,[−∞,−∣t0∗∣] 和 [∣t0∗∣,+∞] 的面積加起來會小於 α,因為 ∣t0∗∣ 會在 tn−2,2α 的右邊。
P-value=PH0(∣t∗∣>∣t0∗∣)=P(∣tn−p∣>∣t0∗∣) ⟹ 在 sig. level α 下,我們拒絕 H0 ⟺ P-value ≤α。並且 P-value 的計算不需要提前知道 α。
ANOVA 表
在簡單線性迴歸的 ANOVA 表中,會做以下的假設檢定:
H0:β1=0H1:β1=0
即檢驗 X 和 Y 是否有顯著的線性關係。
注意到
(t∗)2=(S{b1}b1)2∼tn−pd(χn−p2/(n−p))2(N(0,1)2)dχn−p2/(n−p)χ12/1dF1,n−p
i.e. rej H0 at level α⟺∣t∗∣>tn−p,2α⟺(t∗)2>(tn−p,2α)2⟺(t∗)2>F1,n−p,α

Note
t∗2=S2{b}b2=MSE∑(Xi−Xˉ)21b2=MSEb2∑(Xi−Xˉ)2
and
SSR=∑(Y^i−Yˉ)2=∑(b0+b1Xi−Yˉ)2=∑(Yˉ−b1Xˉ+b1Xi−Yˉ)2=b12∑(Xi−Xˉ)2
⟹t∗2=MSESSR=SSE/(n−p)SSR/(p−1)with p=2 in SLR=MSEMSR∼Fp−1,n−p
因此,在簡單形象迴歸中,對於假設檢定 H0:β1=0 vs H1:β1=0 的 ANOVA 表會如下:
| Source | SS | df | MS=SS/df | F-value | P-value |
|---|
| Regression | SSR | p-1 | MSR | MSR/MSE=f∗ | P(Fp−1,n−p>f∗) |
| Error | SSE | n-p | MSE | | |
| Total | SSTO | n-1 | | | |
Rej H0 at level α⟺F∗≜MSEMSR>Fp−1,n−p,α⟺P-value=P(Fp−1,n−p>F∗)≤α
Remark: 對於單邊檢定
- H0:β1=β1,0 vs H1:β1>β1,0,拒絕 H0⟺S{b1}b1−β1,0>tn−p,α
- H0:β1=β1,0 vs H1:β1<β1,0,拒絕 H0⟺S{b1}b1−β1,0<−tn−p,α
預測值平均的信賴區間
在簡單線性迴歸中,我們拿到數據 Y,X 後,假設我們關注一個新的 Xh 所對應的 Yh。Xh 獨立於得到的數據 X,但它的值可能和 X 中的值相同。
Yh=β0+β1Xh+εh
而我們感興趣的是 E[Yh]=β0+β1Xh。我們可以用 b0,b1 來估計 Yh。
Y^h=b0+b1Xh=∑ciYi+∑kiYiXh=∑(ci+kiXh)Yi
因此 Y^h 是線性估計,並且
E[Y^h]=E[b0]+E[b1]Xh=β0+β1Xh=E[Yh]
所以 Y^h 是 E[Yh] 的線性無偏估計(Linear Unbiased Estimator)。並且 Y^h 同樣是獨立的常態分佈之和,所以
Y^h∼N(β0+β1Xh,σ2{Y^h})
其中
σ2{Y^h}=σ2{∑(ci+KiXh)Yi}=∑(ci+kiXh)2σ2{Yi}=σ2∑(ci+2kiXh+ki2Xh2)=⋯=σ2⋅(n1+∑(Xi−Xˉ)2(Xh−Xˉ)2)
這個結果告訴我們:
- 數據量越大,方差越小
- 數據越分散,��方差越小
- Xh 離中心點越遠,方差越大
這裡我們同樣需要用 MSE 來估計 σ2 的值。
S2{Y^h}≜σ2{Y^h}∣σ2=MSE⟹σ2{Y^h}S2{Y^h}=σ2MSE=σ2SSEn−p1∼χn−p2/(n−p)
⟹S{Y^h}Y^h−E[Yh]=σ{Y^h}⋅σ2{Y^h}S2{Y^h}Y^h−(β0+β1Xh)∵b0⊥SSE,b1⊥SSEdχn−p2/(n−p)N(0,1)上下分佈獨立∼tn−pSLRtn−2
⟹1−α=P(∣tn−p∣≤tn−p,2α)=P(S{Y^h}Y^h−E[Yh]≤tn−p,2α)=P(E[Yh]∈[Y^h±S{Y^h}⋅tn−p,2α])
因此,對於任何給定的 X=Xh,預測平均 E[Yh]=β0+β1Xh 的 1−α conf. int. 是
[Y^h±S{Y^h}⋅tn−p,2α]
預測值的預測區間
如果我們對同樣在 Xh 上的一個獨立的隨機變量 Yh,new 感興趣 ⟹Yh,new⊥Y^h=b0+b1Xh, 並且
Yh,newY^h∼N(β0+β1Xh,σ2)∼N(β0+β1Xh,σ2{Y^h})
⟹Y^h−Yh,new∼N(0,σ2{perd})
with σ2{perd}=σ2{Y^h}+σ2{Yh,new}=σ2⋅(1+n1+∑(Xi−Xˉ)2(Xh−Xˉ)2)>σ2{Y^h}
用 MSE 來估計 σ2 的值,我們可以得到
⟹S{perd}Y^h−Yh,new∼tn−pSLRtn−21−α=P(Yh,new∈[Y^h±S{perd}⋅tn−p,2α])
i.e. [Y^h±S{perd}⋅tn−p,2α] 是 Yh,new 的 1−α 預測區間(Prediction Interval)。
Remark: 在同一個 Xh 上
β0+β1XhYh,new∈[Y^h±S{Y^h}⋅tn−p,2α]∈[Y^h±S{perd}⋅tn−p,2α]with confi. 1−αwith confi. 1−α
⟹(1)⊂(2)
Note: 如果我們感興趣的是 Yˉh,new=m1∑i=1mYh,new,i∼N(β0+β1Xh,mσ2),其中 m 是固定的。
⟹Y^h−Yˉh,new∼N(0,σ2{perd. mean})
with σ2{perd. mean}=σ2{Y^h}+σ2{Yˉh,new}=σ2⋅(m1+n1+∑(Xi−Xˉ)2(Xh−Xˉ)2)>σ2{Y^h}
同樣用 MSE 來估計 σ2 的值
⟹[Y^h±S{perd. mean}⋅tn−p,2α] is 1−α conf. int. for r.v.Yˉh,new(3)
⟹ 在同一個 Xh 上 (1)⊂(3)m=1⊆(2) 並且 (3)m→∞(1)。∵ L.L.N. Yˉh,newPm→∞β0+β1Xh
信賴區帶
我們之前討論的是給定一個 Xh,他所對應的 Yh 可能的範圍。但如果我們現在想要知道整條回歸線的範圍,也就是信賴區帶,那麼我們就沒辦法用之前的方法了。
Remark: 對於任意給定的 Xh=Xh,0,Xh,1,⋯,CI(β0+β1Xh,j) 是 β0+β1Xh,j 的 1−α conf. int. ∀j。
令 Ah,j≜β0+β1Xh,j∈CI(β0+β1Xh,j)⟹P(Ah,j)=1−α,∀j
問題是:P(Ah,0∩Ah,1)=?1−α
並不會,通常 P(Ah,0∩Ah,1)<1−α。如果 Ah,0⊥Ah,1,那麼 P(Ah,0∩Ah,1)=(1−α)2<1−α。
所以我們需要找到一個新的數字 Mα s.t. P(β0+β1X∈[Y^h±MαS{Y^h}],∀X∈R)=1−α。
Note:
∀XY^x=b0+b1X∼N(β0+β1X,σ2{Y^x})with σ2{Y^x}=σ2⋅(n1+∑(Xi−Xˉ)2(X−Xˉ)2)
並且
b0+b1X=Yˉ−b1Xˉ+b1X=Yˉ+b1(X−Xˉ)β0+β1X=E[Yˉ]−β1Xˉ+β1X=E[Yˉ]+β1(X−Xˉ)
i.e.
b0+b1Xβ0+β1X=Yˉ+b1(X−Xˉ)with Yˉ⊥b1∵∑ki⋅n1=0=E[Yˉ]+β1(X−Xˉ)with Yˉ∼N(β0+β1Xˉ,σ2/n)
with Yˉ⊥b1∵∑ki⋅n1=0
and Yˉ∼N(β0+β1Xˉ,σ2/n)b1∼N(β1,∑(Xi−Xˉ)2σ2)
⟹⟺⟺⟺⟺S{Y^x}Y^x−(β0+β1X)≤Mα∀X∈R[S{Y^x}Yˉ−EYˉ+(b1−β1)(X−Xˉ)]2≤Mα2∀X∈RXsup[S{Y^x}Yˉ−EYˉ+(b1−β1)(X−Xˉ)]2≤Mα2XsupMSE⋅(n1+∑(Xi−Xˉ)2(X−Xˉ)2)Yˉ−EYˉ+(b1−β1)(X−Xˉ)2≤Mα2MSE1tsup[n1+∑(Xi−Xˉ)2t2Yˉ−EYˉ+(b1−β1)t]2≤Mα2with t≜X−Xˉ
Note:
t∈Rmax(c+d⋅t)2(a+b⋅t)2=ca2+db2
⟹===MSE1tsup[n1+∑(Xi−Xˉ)2t2Yˉ−EYˉ+(b1−β1)t]2MSE/nYˉ−EYˉ+MSE/∑(Xi−Xˉ)2(b1−β1)2σ2⋅MSE/nσ2Yˉ−EYˉ+σ2⋅MSE/σ2∑(Xi−Xˉ)2(b1−β1)2(n−2)σ2SSE(σ{Yˉ}Y−EYˉˉ)2+(σ{b1}b1−β1)2(*)
Note:
(∗)dn−2χn−22χ12+χ12and each part is independent
∵n−2χn−222χ22∼F2,n−2⟹(∗)∼2⋅F2,n−2
也就是說
⟹1−α=P(β0+β1X∈[Y^x±S{Y^x}Mα])=P(2w≤Mα2)with w∼F2,n−2=P(w≤Mα2/2)Mα=2F2,n−2,α
Walking-Hotelling confidence band for β0+β1X with 1−α confidence level is
[Y^x±2F2,n−2,α⋅S{Y^x}]R squared
R2=SSTOSSR=1−SSTOSSER2 可以衡量 Y 中的變異量有多少可以被 X 解釋。也就是 X 和 Y 之間的線性關係有多強。
Note:
-
R2∈[0,1]
-
R2=1⟺SSE=0⟺ei=0∀i⟺Y^i=Yi∀i
i.e. Y1,⋯,Yn 在一條直線上 ⟹X 可以完全解釋 Y 的變異量。
-
R2=0⟺SSR=0⟺Y^i=Yˉ∀i
i.e. 無論 X 如何變動,Y 的預測值都是一樣的 ⟹X 和 Y 之間沒有線性關係。
注意到:
R2=SSTOSSR=∑(Yi−Yˉ)2∑(Y^i−Yˉ)2=∑(Yi−Yˉ)2b12∑(Xi−Xˉ2)with b1=∑(Xi−Xˉ)2∑(Xi−Xˉ)(Yi−Yˉ)=∑(Xi−Xˉ)2∑(Yi−Yˉ)2(∑(Xi−Xˉ)(Yi−Yˉ))2=[∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)]2
而 X,Y 的樣本協方差是 α∑(Xi��−Xˉ)(Yi−Yˉ),X 的樣本方差是 α∑(Xi−Xˉ)2
⟹∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)=ρ 是 X 和 Y 的樣本相關係數。i.e.
R2=ρ2⟺ρ=∑(Yi−Yˉ)2b1∑(Xi−Xˉ)2
因此 ρ 與 b1 同號。但只有在 SLR 中,R2 和 ρ 才有以上的關係。



