Completely Randomized Design 完全隨機設計的重點在於:讓實驗單位(E.U.)完全隨機的分配 trt 以避免實驗單位間的差異性。這樣的設計方式可以讓我們更容易的去估計 trt 的效應。e.g. 實驗的唯一因素有 3 個 level,每個 level 進行 2 次實驗,共進行 6 次實驗。這 6 次實驗的順序應該是完全隨機,而不是固定的例如 1,2,3,1,2,3。
假設有 k k k n j n_j n j j = 1 , ⋯ , k j=1,\cdots,k j = 1 , ⋯ , k i = 1 , ⋯ , n j i=1,\cdots,n_j i = 1 , ⋯ , n j
Y i j = μ + τ j + ε i j , ε i j ∼ iid N ( 0 , σ ε 2 ) Y_{ij} = \mu + \tau_j + \varepsilon_{ij},\quad \varepsilon_{ij}\overset{\text{iid}}{\sim}N(0,\sigma^2_{\varepsilon}) Y ij = μ + τ j + ε ij , ε ij ∼ iid N ( 0 , σ ε 2 )
Y i j Y_{ij} Y ij j j j i i i μ \mu μ τ j \tau_j τ j j j j ε i j \varepsilon_{ij} ε ij
Note: μ j = μ + τ j \mu_j=\mu+\tau_j μ j = μ + τ j j j j
2 factor CRD Factorial experment
假設有 a a a b b b n i j n_{ij} n ij
Y i j k = μ i j + ε i j k , ε i j k ∼ iid N ( 0 , σ ε 2 ) , i = 1 , ⋯ , a j = 1 , ⋯ , b k = 1 , ⋯ , n i j Y_{ijk}= \mu_{ij}+\varepsilon_{ijk},\quad \varepsilon_{ijk}\overset{\text{iid}}{\sim}N(0,\sigma^2_{\varepsilon}),\quad \begin{align*}
i&=1,\cdots,a\\
j&=1,\cdots,b\\
k&=1,\cdots,n_{ij}
\end{align*} Y ijk = μ ij + ε ijk , ε ijk ∼ iid N ( 0 , σ ε 2 ) , i j k = 1 , ⋯ , a = 1 , ⋯ , b = 1 , ⋯ , n ij ⟹ μ i j = E ( Y i j k ) = E ( Y ∣ A = i , B = j ) \implies \mu_{ij}=E(Y_{ijk})=E(Y|A=i,B=j) ⟹ μ ij = E ( Y ijk ) = E ( Y ∣ A = i , B = j ) Factorial vs. OFAT
Factorial 實驗是對每個 treatment 都進行至少一次實驗,而 OFAT (One Factor At a Time) 則通過與選擇的 baseline trt 進行比較,來估計其他 trt 的效應,具體有以下步驟:
選擇一個 baseline trt
固定 B 因素,遍歷 A 因素的所有水平 => 得到最佳的 A 水平,記作 i A i_A i A
固定 A 因素,遍歷 B 因素的所有水平 => 得到最佳的 B 水平,記作 i B i_B i B
得到最佳 trt 組合 ( i A , i B ) (i_A,i_B) ( i A , i B )
OFAT 並不會查看所有 trt 的組合,因此可能會錯過一些重要的交互作用。( i A , j B ) (i_A, j_B) ( i A , j B )
EX: Y 為某集成電路的電流量,有以下因素,假設希望數值越大越好:
A: 海拔(0 k , 3 k 0^k, 3^k 0 k , 3 k
B: 溫度(25, 55)
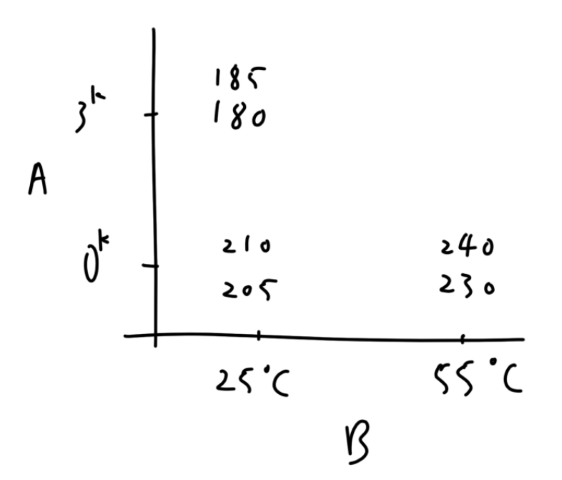
以 OFAT 方式實驗收集到以下數據:
假設 baseline trt 為 ( 0 k , 25 ) (0^k, 25) ( 0 k , 25 )
固定 B 因素,Y ˉ : 207.5 → 235 ⇒ 27.5 \bar{Y}:207.5\to 235\Rightarrow 27.5 Y ˉ : 207.5 → 235 ⇒ 27.5
固定 A 因素,Y ˉ : 207.5 → 182.5 ⇒ − 25 \bar{Y}:207.5\to 182.5\Rightarrow -25 Y ˉ : 207.5 → 182.5 ⇒ − 25
得到結論,trt ( 0 k , 55 ) (0^k, 55) ( 0 k , 55 )
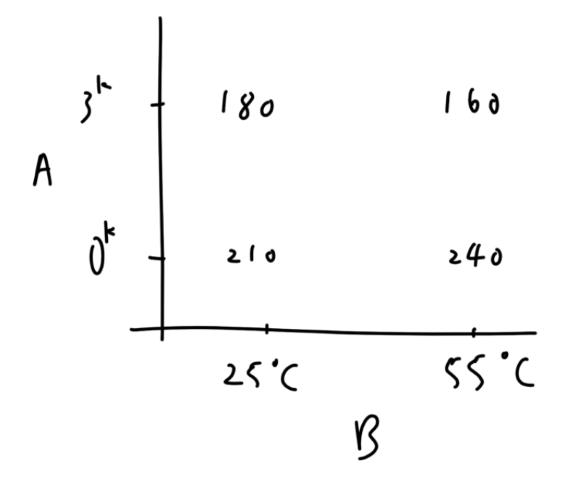
以 Factorial 方式實驗收集到以下數據:
比較所有觀測值,得到結論,trt ( 0 k , 55 ) (0^k, 55) ( 0 k , 55 )
兩種方法得到了相同的結論,但 Factorial 只需要 4 次實驗,OFAT 需要 6 次實驗。
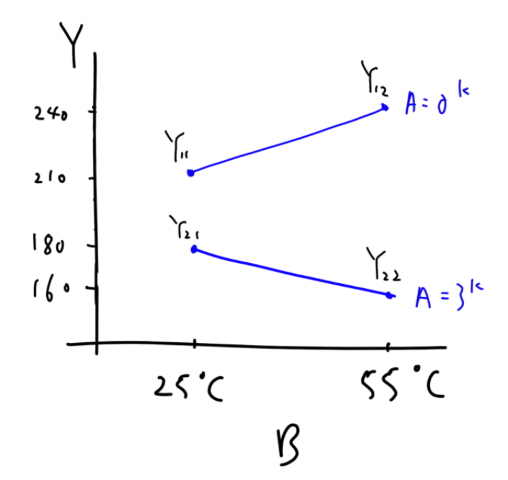
如果我們將 B 因素設為 x 軸,觀察值設為 y 軸,並將 A 因素相同 level 的點連接起來,可以得到以下圖形:
可以從圖中看到 A 和 B 之間存在交互左右,因為不同 A 水平下會影響線條的斜率。而這是 OFAT 無法發現的。
Graphical display of data
Y i j k = μ + τ i + β j + ( τ β ) i j + ε i j k Y_{ijk}=\mu+\tau_i+\beta_j+(\tau\beta)_{ij}+\varepsilon_{ijk} Y ijk = μ + τ i + β j + ( τ β ) ij + ε ijk 我們可以通過圖形化的方式來展示 μ i j \mu_{ij} μ ij μ i j \mu_ij μ i j
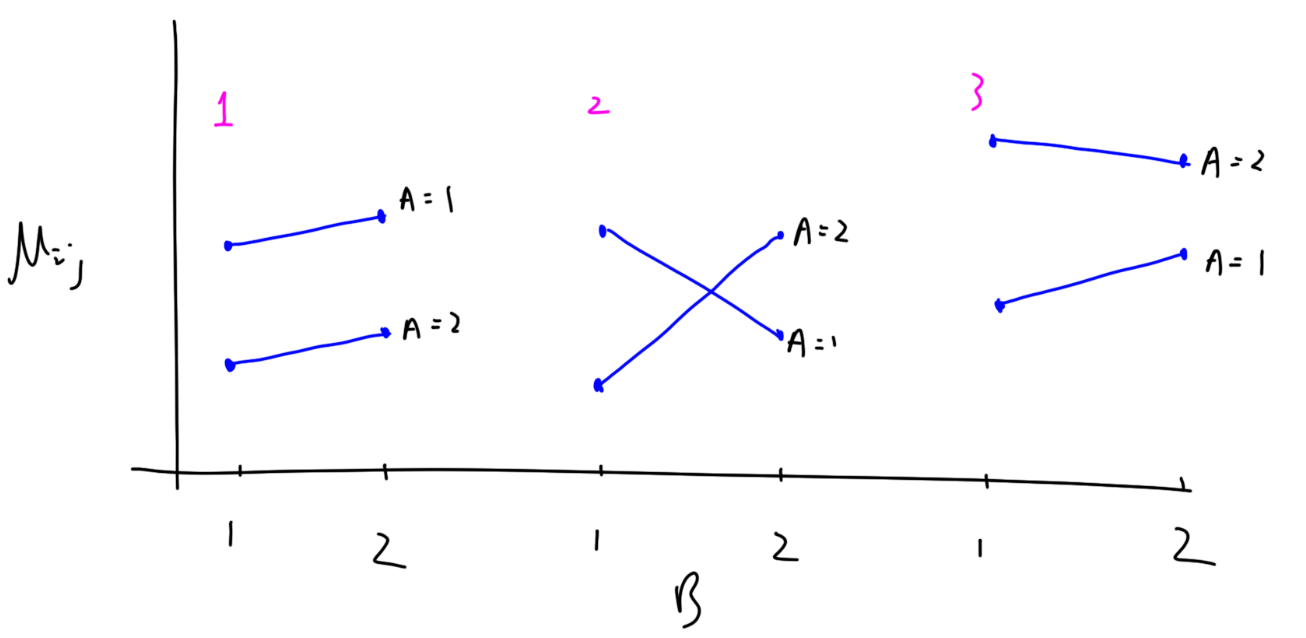
如果 A 的 level 數 a = 2 a=2 a = 2 b = 2 b=2 b = 2
平行(Parallel)
⟹ \implies ⟹
⟹ \implies ⟹
相交(Crossed)
⟹ \implies ⟹
⟹ \implies ⟹
介於 Parallel 和 Crossed 之間
⟹ \implies ⟹
Note:μ i j \mu_{ij} μ ij
μ i j ^ = 1 n i j ∑ k = 1 n i j Y i j k = Y ˉ i j ⋅ \widehat{\mu_{ij}}=\frac{1}{n_{ij}}\sum_{k=1}^{n_{ij}}Y_{ijk}=\bar{Y}_{ij\cdot} μ ij = n ij 1 k = 1 ∑ n ij Y ijk = Y ˉ ij ⋅ Interaction
Note: A 與 B 如果不存在交互作用 ⟺ \iff ⟺
μ i j − μ i ′ j = μ i j ′ − μ i ′ j ′ ∀ i ≠ i ′ , j ≠ j ′ \mu_{ij}-\mu_{i'j}=\mu_{ij'}-\mu_{i'j'}\quad\forall i\neq i', j\neq j' μ ij − μ i ′ j = μ i j ′ − μ i ′ j ′ ∀ i = i ′ , j = j ′ μ i j − μ i j ′ = μ i ′ j − μ i ′ j ′ ∀ i ≠ i ′ , j ≠ j ′ \mu_{ij}-\mu_{ij'}=\mu_{i'j}-\mu_{i'j'}\quad\forall i\neq i', j\neq j' μ ij − μ i j ′ = μ i ′ j − μ i ′ j ′ ∀ i = i ′ , j = j ′
合併以上兩點得到:
μ i j + μ i ′ j ′ − μ i j ′ − μ i ′ j = 0 ∀ i ≠ i ′ , j ≠ j ′ ⟹ 1 a ⋅ b ∑ i ′ = 1 a ∑ j ′ = 1 b ( μ i j + μ i ′ j ′ − μ i j ′ − μ i ′ j ) = 0 ∀ i = 1 , ⋯ , a , j = 1 , ⋯ , b ⟹ μ i j + μ ˉ ⋅ ⋅ − μ ˉ i ⋅ − μ ˉ ⋅ j = 0 ∀ i = 1 , ⋯ , a , j = 1 , ⋯ , b \begin{align*}
&\mu_{ij}+\mu_{i'j'}-\mu_{ij'}-\mu_{i'j}=0 \quad\forall i\neq i', j\neq j'\\
\implies&\frac{1}{a\cdot b}\sum_{i'=1}^a\sum_{j'=1}^b(\mu_{ij}+\mu_{i'j'}-\mu_{ij'}-\mu_{i'j})=0\quad\forall i=1,\cdots,a, j=1,\cdots,b\\
\implies&\mu_{ij}+\bar{\mu}_{\cdot\cdot}-\bar{\mu}_{i\cdot}-\bar{\mu}_{\cdot j}=0\quad \forall i=1,\cdots,a, j=1,\cdots,b
\end{align*} ⟹ ⟹ μ ij + μ i ′ j ′ − μ i j ′ − μ i ′ j = 0 ∀ i = i ′ , j = j ′ a ⋅ b 1 i ′ = 1 ∑ a j ′ = 1 ∑ b ( μ ij + μ i ′ j ′ − μ i j ′ − μ i ′ j ) = 0 ∀ i = 1 , ⋯ , a , j = 1 , ⋯ , b μ ij + μ ˉ ⋅⋅ − μ ˉ i ⋅ − μ ˉ ⋅ j = 0 ∀ i = 1 , ⋯ , a , j = 1 , ⋯ , b with μ ˉ = μ ˉ ⋅ ⋅ = 1 a ⋅ b ∑ i = 1 a ∑ j = 1 b μ i j , μ ˉ i = μ ˉ i ⋅ = 1 b ∑ j = 1 b μ i j , μ ˉ j = μ ˉ ⋅ j = 1 a ∑ i = 1 a μ i j \text{with}\quad \bar{\mu}=\bar{\mu}_{\cdot\cdot}=\frac{1}{a\cdot b}\sum_{i=1}^a\sum_{j=1}^b\mu_{ij},\quad \bar{\mu}_i=\bar{\mu}_{i\cdot}=\frac{1}{b}\sum_{j=1}^b\mu_{ij},\quad \bar{\mu}_j=\bar{\mu}_{\cdot j}=\frac{1}{a}\sum_{i=1}^a\mu_{ij} with μ ˉ = μ ˉ ⋅⋅ = a ⋅ b 1 i = 1 ∑ a j = 1 ∑ b μ ij , μ ˉ i = μ ˉ i ⋅ = b 1 j = 1 ∑ b μ ij , μ ˉ j = μ ˉ ⋅ j = a 1 i = 1 ∑ a μ ij
μ \mu μ μ i \mu_i μ i μ j \mu_j μ j
Remark: H 0 : μ i j + μ ˉ − μ ˉ i − μ ˉ j = 0 ∀ i , j H_0:\mu_{ij}+\bar{\mu}-\bar{\mu}_i-\bar{\mu}_j=0 \forall i,j H 0 : μ ij + μ ˉ − μ ˉ i − μ ˉ j = 0∀ i , j H 0 : H_0: H 0 :
A B i j = μ i j + μ − μ i − μ j AB_{ij}=\mu_{ij}+\mu-\mu_i-\mu_j A B ij = μ ij + μ − μ i − μ j is called the interation of A = i A=i A = i B = j B=j B = j
Main effect: A 因素從 level i → i ′ i\to i' i → i ′
1 b ∑ j = 1 b μ i j − 1 b ∑ j = 1 b μ i ′ j = μ ˉ i ⋅ − μ ˉ i ′ ⋅ = μ i − μ i ′ = ( μ i − μ ) − ( μ i ′ − μ ) = A i − A i ′ \begin{align*}
\frac{1}{b}\sum_{j=1}^b\mu_{ij}-\frac{1}{b}\sum_{j=1}^b\mu_{i'j}&=\bar{\mu}_{i\cdot}-\bar{\mu}_{i'\cdot}=\mu_i-\mu_{i'}\\
&=(\mu_i-\mu)-(\mu_{i'}-\mu)\\
&=A_i-A_{i'}
\end{align*} b 1 j = 1 ∑ b μ ij − b 1 j = 1 ∑ b μ i ′ j = μ ˉ i ⋅ − μ ˉ i ′ ⋅ = μ i − μ i ′ = ( μ i − μ ) − ( μ i ′ − μ ) = A i − A i ′ Main effect of A at level i ≜ μ i − μ i = 1 , ⋯ , a i\triangleq \mu_i-\mu\quad i=1,\cdots,a i ≜ μ i − μ i = 1 , ⋯ , a A i A_i A i
Main effect of B at level j ≜ μ j − μ j = 1 , ⋯ , b j\triangleq \mu_j-\mu\quad j=1,\cdots,b j ≜ μ j − μ j = 1 , ⋯ , b B j B_j B j
模型也可以由以上定義進行解釋:
Y i j k = μ i j + ε ( i j ) k = μ + ( μ i j + μ − μ i − μ j ) + ( μ i − μ ) + ( μ j − μ ) + ε ( i j ) k = μ + A i + B j + A B i j + ε ( i j ) k \begin{align*}
Y_{ijk}&=\mu_{ij}+\varepsilon_{(ij)k}\\
&=\mu+(\mu_{ij}+\mu-\mu_i-\mu_j)+(\mu_i-\mu)+(\mu_j-\mu)+\varepsilon_{(ij)k}\\
&=\mu+A_i+B_j+AB_{ij}+\varepsilon_{(ij)k}
\end{align*} Y ijk = μ ij + ε ( ij ) k = μ + ( μ ij + μ − μ i − μ j ) + ( μ i − μ ) + ( μ j − μ ) + ε ( ij ) k = μ + A i + B j + A B ij + ε ( ij ) k Fixed and Random effects
Effect 有兩種類型:
Fixed effect:對特定的固定值感興趣。
Random effect:對母體感興趣,而樣本只是其中的一部分。
對於不同類型效應的組合,可以形成不同的實驗模型,並且會對其加上不同的限制:
A, B both fixed effect ⟺ \iff ⟺ fixed model
⟹ \implies ⟹
∑ i = 1 a A i = 0 , ∑ j = 1 b B j = 0 \sum_{i=1}^aA_i=0,\quad \sum_{j=1}^bB_j=0 i = 1 ∑ a A i = 0 , j = 1 ∑ b B j = 0 ∑ i = 1 a A B i j = 0 , ∀ j , ∑ j = 1 b A B i j = 0 , ∀ i \sum_{i=1}^aAB_{ij}=0,\quad\forall j,\quad \sum_{j=1}^bAB_{ij}=0,\quad\forall i i = 1 ∑ a A B ij = 0 , ∀ j , j = 1 ∑ b A B ij = 0 , ∀ i 這代表:A 有 a − 1 a-1 a − 1 b − 1 b-1 b − 1 ( a − 1 ) ( b − 1 ) (a-1)(b-1) ( a − 1 ) ( b − 1 )
A, B both random effect ⟺ \iff ⟺ random model
⟹ \implies ⟹
A 1 , ⋯ , A a ∼ iid N ( 0 , σ A 2 ) , B 1 , ⋯ , B b ∼ iid N ( 0 , σ B 2 ) A_1,\cdots,A_a\overset{\text{iid}}{\sim}N(0,\sigma^2_A),\quad B_1,\cdots,B_b\overset{\text{iid}}{\sim}N(0,\sigma^2_B) A 1 , ⋯ , A a ∼ iid N ( 0 , σ A 2 ) , B 1 , ⋯ , B b ∼ iid N ( 0 , σ B 2 ) A B i j ∼ iid N ( 0 , σ A B 2 ) i = 1 , ⋯ , a , j = 1 , ⋯ , b AB_{ij}\overset{\text{iid}}{\sim}N(0,\sigma^2_{AB})\quad i=1,\cdots,a, j=1,\cdots,b A B ij ∼ iid N ( 0 , σ A B 2 ) i = 1 , ⋯ , a , j = 1 , ⋯ , b 且 A i ⊥ B i ⊥ A B i j ⊥ ε ( i j ) k A_i\perp B_i\perp AB_{ij}\perp \varepsilon_{(ij)k} A i ⊥ B i ⊥ A B ij ⊥ ε ( ij ) k
Note: σ A 2 = 0 ⟹ A 1 = ⋯ = A a = 0 \sigma^2_A=0\implies A_1=\cdots=A_a=0 σ A 2 = 0 ⟹ A 1 = ⋯ = A a = 0
One fixed, one random ⟺ \iff ⟺ mixed model
⟹ \implies ⟹
∑ A i = 0 , B 1 , ⋯ , B b ∼ iid N ( 0 , σ B 2 ) , A B i j ∼ iid N ( 0 , σ A B 2 ) \sum A_i=0,\quad B_1,\cdots,B_b\overset{\text{iid}}{\sim}N(0,\sigma^2_B), \quad AB_{ij}\overset{\text{iid}}{\sim}N(0,\sigma^2_{AB}) ∑ A i = 0 , B 1 , ⋯ , B b ∼ iid N ( 0 , σ B 2 ) , A B ij ∼ iid N ( 0 , σ A B 2 ) with ∑ i = 1 a A i B j = 0 ∀ j , ∑ j = 1 b A i B j ≠ 0 ∀ i usually \text{with } \sum_{i=1}^a A_iB_j=0\quad\forall j,\quad \sum_{j=1}^b A_iB_j\neq 0\quad \forall i\quad \text{ usually} with i = 1 ∑ a A i B j = 0 ∀ j , j = 1 ∑ b A i B j = 0 ∀ i usually
以上三種不同的模型有相同的 SS, e.g.
S S total = ∑ i = 1 a ∑ j = 1 b ∑ k = 1 n i j ( Y i j k − Y ˉ ⋅ ⋅ ⋅ ) 2 S S A = ∑ i = 1 a ∑ j = 1 b ∑ k = 1 n i j ( Y ˉ i ⋅ ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 S S B = ∑ i = 1 a ∑ j = 1 b ∑ k = 1 n i j ( Y ˉ ⋅ j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 S S A B = ∑ i = 1 a ∑ j = 1 b ∑ k = 1 n i j ( Y ˉ i j ⋅ − Y ˉ i ⋅ ⋅ − Y ˉ ⋅ j ⋅ + Y ˉ ⋅ ⋅ ⋅ ) 2 \begin{align*}
SS_{\text{total}}&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^{n_{ij}}(Y_{ijk}-\bar{Y}_{\cdot\cdot\cdot})^2\\
SS_A&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^{n_{ij}}(\bar{Y}_{i\cdot\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2\\
SS_B&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^{n_{ij}}(\bar{Y}_{\cdot j\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2\\
SS_{AB}&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^{n_{ij}}(\bar{Y}_{ij\cdot}-\bar{Y}_{i\cdot\cdot}-\bar{Y}_{\cdot j\cdot}+\bar{Y}_{\cdot\cdot\cdot})^2
\end{align*} S S total S S A S S B S S A B = i = 1 ∑ a j = 1 ∑ b k = 1 ∑ n ij ( Y ijk − Y ˉ ⋅⋅⋅ ) 2 = i = 1 ∑ a j = 1 ∑ b k = 1 ∑ n ij ( Y ˉ i ⋅⋅ − Y ˉ ⋅⋅⋅ ) 2 = i = 1 ∑ a j = 1 ∑ b k = 1 ∑ n ij ( Y ˉ ⋅ j ⋅ − Y ˉ ⋅⋅⋅ ) 2 = i = 1 ∑ a j = 1 ∑ b k = 1 ∑ n ij ( Y ˉ ij ⋅ − Y ˉ i ⋅⋅ − Y ˉ ⋅ j ⋅ + Y ˉ ⋅⋅⋅ ) 2 ( Y i j k − Y ˉ ⋅ ⋅ ⋅ ) 2 = ( Y i j k − Y ˉ i j ⋅ + Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 (Y_{ijk}-\bar{Y}_{\cdot\cdot\cdot})^2=(Y_{ijk}-\bar{Y}_{ij\cdot}+\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2 ( Y ijk − Y ˉ ⋅⋅⋅ ) 2 = ( Y ijk − Y ˉ ij ⋅ + Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ ) 2 ∑ k n i j ( Y i j k Y ˉ i j ⋅ − Y i j k Y ˉ ⋅ ⋅ ⋅ − Y ˉ i j ⋅ 2 + Y ˉ i j ⋅ Y ˉ ⋅ ⋅ ⋅ ) = n i j Y ˉ i j ⋅ 2 − n i j Y ˉ i j ⋅ Y ˉ ⋅ ⋅ ⋅ − n i j Y ˉ i j ⋅ 2 + n i j Y ˉ i j ⋅ Y ˉ ⋅ ⋅ ⋅ = 0 \sum_k^{n_{ij}}(Y_{ijk}\bar{Y}_{ij\cdot}-Y_{ijk}\bar{Y}_{\cdot\cdot\cdot}-\bar{Y}_{ij\cdot}^2+\bar{Y}_{ij\cdot}\bar{Y}_{\cdot\cdot\cdot})=n_{ij}\bar{Y}_{ij\cdot}^2-n_{ij}\bar{Y}_{ij\cdot}\bar{Y}_{\cdot\cdot\cdot}-n_{ij}\bar{Y}_{ij\cdot}^2+n_{ij}\bar{Y}_{ij\cdot}\bar{Y}_{\cdot\cdot\cdot}=0 k ∑ n ij ( Y ijk Y ˉ ij ⋅ − Y ijk Y ˉ ⋅⋅⋅ − Y ˉ ij ⋅ 2 + Y ˉ ij ⋅ Y ˉ ⋅⋅⋅ ) = n ij Y ˉ ij ⋅ 2 − n ij Y ˉ ij ⋅ Y ˉ ⋅⋅⋅ − n ij Y ˉ ij ⋅ 2 + n ij Y ˉ ij ⋅ Y ˉ ⋅⋅⋅ = 0 ⟹ S S total = ∑ i ∑ j ∑ k ( Y i j k − Y ˉ i j ⋅ ) 2 + ∑ i ∑ j ∑ k ( Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 + 2 ∑ i ∑ j ∑ k ( Y i j k − Y ˉ i j ⋅ ) ( Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) ⏟ = 0 = ∑ i ∑ j ∑ k ( Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 + ∑ i ∑ j ∑ k ( Y i j k − Y ˉ i j ⋅ ) 2 = S S trt + S S error \begin{align*}
\implies SS_{\text{total}}=&\sum_i\sum_j\sum_k(Y_{ijk}-\bar{Y}_{ij\cdot})^2+\sum_i\sum_j\sum_k(\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2+2\sum_i\sum_j\underbrace{\sum_k(Y_{ijk}-\bar{Y}_{ij\cdot})(\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot})}_{=0}\\
=&\sum_i\sum_j\sum_k(\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2+\sum_i\sum_j\sum_k(Y_{ijk}-\bar{Y}_{ij\cdot})^2\\
=&SS_{\text{trt}}+SS_{\text{error}}
\end{align*} ⟹ S S total = = = i ∑ j ∑ k ∑ ( Y ijk − Y ˉ ij ⋅ ) 2 + i ∑ j ∑ k ∑ ( Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ ) 2 + 2 i ∑ j ∑ = 0 k ∑ ( Y ijk − Y ˉ ij ⋅ ) ( Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ ) i ∑ j ∑ k ∑ ( Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ ) 2 + i ∑ j ∑ k ∑ ( Y ijk − Y ˉ ij ⋅ ) 2 S S trt + S S error ( Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 = [ ( Y ˉ i ⋅ ⋅ − Y ˉ ⋅ ⋅ ⋅ ) + ( Y ˉ ⋅ j ⋅ − Y ˉ ⋅ ⋅ ⋅ ) + ( Y ˉ i j ⋅ − Y ˉ ⋅ ⋅ ⋅ − Y ˉ ⋅ j ⋅ + Y ˉ ⋅ ⋅ ⋅ ) ] 2 (\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2=[(\bar{Y}_{i\cdot\cdot}-\bar{Y}_{\cdot\cdot\cdot})+(\bar{Y}_{\cdot j\cdot}-\bar{Y}_{\cdot\cdot\cdot})+(\bar{Y}_{ij\cdot}-\bar{Y}_{\cdot\cdot\cdot}-\bar{Y}_{\cdot j\cdot} +\bar{Y}_{\cdot\cdot\cdot})]^2 ( Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ ) 2 = [( Y ˉ i ⋅⋅ − Y ˉ ⋅⋅⋅ ) + ( Y ˉ ⋅ j ⋅ − Y ˉ ⋅⋅⋅ ) + ( Y ˉ ij ⋅ − Y ˉ ⋅⋅⋅ − Y ˉ ⋅ j ⋅ + Y ˉ ⋅⋅⋅ ) ] 2 ⟹ S S trt = S S A + S S B + S S A B \implies SS_{\text{trt}}=SS_A+SS_B+SS_{AB} ⟹ S S trt = S S A + S S B + S S A B 三種不同的模型都可以用相同的公式計算以上 SS ,但對於檢驗 H 0 : H_0: H 0 :
ANOVA
One-factor CRD
Level's # = k = # of trt's
Y i j = μ i + ε i j , i = 1 ⋯ , k , j = 1 , ⋯ , n i ( = n if balanced ) = μ + τ i + ε i j , ε i j ∼ iid N ( 0 , �σ ε 2 ) \begin{align*}
Y_{ij}&=\mu_i+\varepsilon_{ij},\quad i=1\cdots,k, j=1,\cdots,n_i(=n\text{ if balanced})\\
&=\mu+\tau_i+\varepsilon_{ij},\quad \varepsilon_{ij}\overset{\text{iid}}{\sim}N(0,\sigma^2_{\varepsilon})
\end{align*} Y ij = μ i + ε ij , i = 1 ⋯ , k , j = 1 , ⋯ , n i ( = n if balanced ) = μ + τ i + ε ij , ε ij ∼ iid N ( 0 , σ ε 2 )
μ \mu μ τ i \tau_i τ i i i i ε i j \varepsilon_{ij} ε ij
Recall:
τ i { fixed ⟹ ∑ τ i = 0 random ⟹ τ i ∼ iid N ( 0 , σ τ 2 ) \tau_i\begin{cases}
\text{fixed}&\implies \sum\tau_i=0\\
\text{random}&\implies \tau_i\overset{\text{iid}}{\sim}N(0,\sigma^2_{\tau})
\end{cases} τ i { fixed random ⟹ ∑ τ i = 0 ⟹ τ i ∼ iid N ( 0 , σ τ 2 ) ⟹ E ( S S E ) = E [ ∑ i = 1 k ∑ j = 1 n ( Y i j − Y ˉ i ⋅ ) 2 ] = E [ ∑ i = 1 k ∑ j = 1 n ( μ + τ i + ε i j − μ − τ i − ε ˉ i ⋅ ) 2 ] = E [ ∑ i = 1 k ∑ j = 1 n ( ε i j − ε ˉ i ⋅ ) 2 ] \begin{align*}
\implies E(SS_E)&=E\left[\sum_{i=1}^k\sum_{j=1}^n(Y_{ij}-\bar{Y}_{i\cdot})^2 \right]\\
&=E\left[\sum_{i=1}^k\sum_{j=1}^n(\mu+\tau_i+\varepsilon_{ij}-\mu-\tau_i-\bar{\varepsilon}_{i\cdot})^2 \right]\\
&=E\left[\sum_{i=1}^k\sum_{j=1}^n(\varepsilon_{ij}-\bar{\varepsilon}_{i\cdot})^2 \right]\\
\end{align*} ⟹ E ( S S E ) = E [ i = 1 ∑ k j = 1 ∑ n ( Y ij − Y ˉ i ⋅ ) 2 ] = E [ i = 1 ∑ k j = 1 ∑ n ( μ + τ i + ε ij − μ − τ i − ε ˉ i ⋅ ) 2 ] = E [ i = 1 ∑ k j = 1 ∑ n ( ε ij − ε ˉ i ⋅ ) 2 ] fixed i i i ε i 1 , ε i 2 , ⋯ , ε i n ∼ iid N ( 0 , σ ε 2 ) \varepsilon_{i1},\varepsilon_{i2},\cdots,\varepsilon_{in}\overset{\text{iid}}{\sim}N(0,\sigma^2_{\varepsilon}) ε i 1 , ε i 2 , ⋯ , ε in ∼ iid N ( 0 , σ ε 2 )
E [ ∑ j = 1 n ( ε i j − ε ˉ i ⋅ ) 2 σ ε 2 ] = E [ χ n − 1 2 ] = n − 1 E\left[\sum_{j=1}^n\frac{(\varepsilon_{ij}-\bar{\varepsilon}_{i\cdot})^2}{\sigma_\varepsilon^2} \right]=E[\chi^2_{n-1}]=n-1 E [ j = 1 ∑ n σ ε 2 ( ε ij − ε ˉ i ⋅ ) 2 ] = E [ χ n − 1 2 ] = n − 1 ⟹ E ( S S E ) = ∑ i = 1 k ( n − 1 ) σ ε 2 = k ( n − 1 ) σ ε 2 \implies E(SS_E)=\sum_{i=1}^k(n-1)\sigma^2_{\varepsilon}=k(n-1)\sigma^2_{\varepsilon} ⟹ E ( S S E ) = i = 1 ∑ k ( n − 1 ) σ ε 2 = k ( n − 1 ) σ ε 2 M S E = S S E d f = S S E k ( n − 1 ) ⟹ E ( M S E ) = E ( S S E ) k ( n − 1 ) = σ ε 2 MS_E=\frac{SS_E}{df}=\frac{SS_E}{k(n-1)}\implies E(MS_E)=\frac{E(SS_E)}{k(n-1)}=\sigma^2_{\varepsilon} M S E = df S S E = k ( n − 1 ) S S E ⟹ E ( M S E ) = k ( n − 1 ) E ( S S E ) = σ ε 2 ⟹ M S E \implies MS_E ⟹ M S E σ ε 2 \sigma^2_{\varepsilon} σ ε 2
E ( S S t r t ) = E [ ∑ i = 1 k ∑ j = 1 n ( Y ˉ i ⋅ − Y ˉ ⋅ ⋅ ) 2 ] = E [ ∑ i k n ( Y ˉ i ⋅ − Y ˉ ⋅ ⋅ ) 2 ] = E [ ∑ i = 1 k n ( μ − τ i + ε ˉ i ⋅ − μ − τ ˉ ⋅ − ε ˉ ⋅ ⋅ ) 2 ] = E [ ∑ i = 1 k n [ ( τ i − τ ˉ ⋅ ) 2 + ( ε ˉ i ⋅ − τ ˉ ⋅ ⋅ ) 2 + 2 ( τ i − τ ˉ ⋅ ) ( ε ˉ i ⋅ − ε ˉ ⋅ ⋅ ) ] ] = n E [ ∑ i = 1 k ( τ i − τ ˉ ⋅ ) 2 ] + n E [ ∑ i = 1 k ( ε ˉ i ⋅ − ε ˉ ⋅ ⋅ ) 2 ] + 2 n E [ ∑ i = 1 k ( τ i − τ ˉ ⋅ ) ( ε ˉ i ⋅ − ε ˉ ⋅ ⋅ ) ] ⏟ = 0 , τ i : fixed or random \begin{align*}
E(SS_{trt})&=E\left[\sum_{i=1}^k\sum_{j=1}^n(\bar{Y}_{i\cdot}-\bar{Y}_{\cdot\cdot})^2 \right]\\
&=E\left[\sum_i^k n(\bar{Y}_{i\cdot}-\bar{Y}_{\cdot\cdot})^2 \right]\\
&=E\left[\sum_{i=1}^k n(\mu-\tau_i+\bar{\varepsilon}_{i\cdot}-\mu-\bar{\tau}_{\cdot}-\bar{\varepsilon}_{\cdot\cdot})^2 \right]\\
&=E\left[\sum_{i=1}^k n[(\tau_i-\bar{\tau}_{\cdot})^2+(\bar{\varepsilon}_{i\cdot}-\bar{\tau}_{\cdot\cdot})^2+2(\tau_i-\bar{\tau}_{\cdot})(\bar{\varepsilon}_{i\cdot}-\bar{\varepsilon}_{\cdot\cdot})] \right]\\
&=nE\left[\sum_{i=1}^k(\tau_i-\bar{\tau}_{\cdot})^2 \right]+nE\left[\sum_{i=1}^k(\bar{\varepsilon}_{i\cdot}-\bar{\varepsilon}_{\cdot\cdot})^2 \right]+2n\underbrace{E\left[\sum_{i=1}^k(\tau_i-\bar{\tau}_{\cdot})(\bar{\varepsilon}_{i\cdot}-\bar{\varepsilon}_{\cdot\cdot}) \right]}_{=0,\quad \tau_i: \text{ fixed or random}}
\end{align*} E ( S S t r t ) = E [ i = 1 ∑ k j = 1 ∑ n ( Y ˉ i ⋅ − Y ˉ ⋅⋅ ) 2 ] = E [ i ∑ k n ( Y ˉ i ⋅ − Y ˉ ⋅⋅ ) 2 ] = E [ i = 1 ∑ k n ( μ − τ i + ε ˉ i ⋅ − μ − τ ˉ ⋅ − ε ˉ ⋅⋅ ) 2 ] = E [ i = 1 ∑ k n [( τ i − τ ˉ ⋅ ) 2 + ( ε ˉ i ⋅ − τ ˉ ⋅⋅ ) 2 + 2 ( τ i − τ ˉ ⋅ ) ( ε ˉ i ⋅ − ε ˉ ⋅⋅ )] ] = n E [ i = 1 ∑ k ( τ i − τ ˉ ⋅ ) 2 ] + n E [ i = 1 ∑ k ( ε ˉ i ⋅ − ε ˉ ⋅⋅ ) 2 ] + 2 n = 0 , τ i : fixed or random E [ i = 1 ∑ k ( τ i − τ ˉ ⋅ ) ( ε ˉ i ⋅ − ε ˉ ⋅⋅ ) ] ε ˉ 1 ⋅ , ⋯ , ε ˉ k ⋅ ∼ iid N ( 0 , σ ε 2 n ) ⟹ ∑ i = 1 k ( ε ˉ i ⋅ − ε ˉ ⋅ ⋅ ) 2 σ ε 2 / n ∼ χ k − 1 2 ⟹ E [ ∑ i = 1 k ( ε ˉ i ⋅ − ε ˉ ⋅ ⋅ ) 2 ] = ( k − 1 ) σ ε 2 \bar{\varepsilon}_{1\cdot},\cdots,\bar{\varepsilon}_{k\cdot}\overset{\text{iid}}{\sim}N(0,\frac{\sigma^2_{\varepsilon}}{n})\implies\sum_{i=1}^k \frac{(\bar{\varepsilon}_{i\cdot}-\bar{\varepsilon}_{\cdot\cdot})^2}{\sigma^2_\varepsilon/n}\sim\chi^2_{k-1}\implies E\left[\sum_{i=1}^k(\bar{\varepsilon}_{i\cdot}-\bar{\varepsilon}_{\cdot\cdot})^2 \right]=(k-1)\sigma^2_{\varepsilon} ε ˉ 1 ⋅ , ⋯ , ε ˉ k ⋅ ∼ iid N ( 0 , n σ ε 2 ) ⟹ i = 1 ∑ k σ ε 2 / n ( ε ˉ i ⋅ − ε ˉ ⋅⋅ ) 2 ∼ χ k − 1 2 ⟹ E [ i = 1 ∑ k ( ε ˉ i ⋅ − ε ˉ ⋅⋅ ) 2 ] = ( k − 1 ) σ ε 2 n E [ ∑ i = 1 k ( τ i − τ ˉ ⋅ ) 2 ] = { n ∑ i = 1 k τ i 2 τ i : fixed ⟹ ∑ τ i = 0 ⟹ τ ˉ ⋅ = 0 n ( k − 1 ) σ τ 2 τ i : random ⟹ ∑ k ( τ i − τ ˉ ⋅ ) 2 σ τ 2 ∼ χ k − 1 2 nE\left[\sum_{i=1}^k(\tau_i-\bar{\tau}_{\cdot})^2 \right]=\begin{cases}
n\sum_{i=1}^k\tau_i^2 & \tau_i: \text{ fixed}\implies\sum\tau_i=0\implies\bar{\tau}_{\cdot}=0\\
n(k-1)\sigma^2_{\tau} & \tau_i: \text{ random}\implies \sum^k\frac{(\tau_i-\bar{\tau}_\cdot)^2}{\sigma^2_\tau}\sim\chi^2_{k-1}
\end{cases} n E [ i = 1 ∑ k ( τ i − τ ˉ ⋅ ) 2 ] = { n ∑ i = 1 k τ i 2 n ( k − 1 ) σ τ 2 τ i : fixed ⟹ ∑ τ i = 0 ⟹ τ ˉ ⋅ = 0 τ i : random �⟹ ∑ k σ τ 2 ( τ i − τ ˉ ⋅ ) 2 ∼ χ k − 1 2 ⟹ E ( S S t r t ) = { ( k − 1 ) σ ε 2 + n ∑ i = 1 k τ i 2 τ i : fixed ( k − 1 ) σ ε 2 + n ( k − 1 ) σ τ 2 τ i : random = { ( k − 1 ) σ ε 2 + n ( k − 1 ) ∑ i = 1 k τ i 2 k − 1 τ i : fixed, ∑ i = 1 k τ i 2 k − 1 donated by ϕ τ ( k − 1 ) σ ε 2 + n ( k − 1 ) σ τ 2 τ i : random \begin{align*}
\implies E(SS_{trt})&=\begin{cases}
(k-1)\sigma_\varepsilon^2+n\sum_{i=1}^k\tau_i^2 & \tau_i: \text{ fixed}\\
(k-1)\sigma_\varepsilon^2+n(k-1)\sigma^2_{\tau} & \tau_i: \text{ random}
\end{cases}\\
&=\begin{cases}
(k-1)\sigma_\varepsilon^2+n(k-1)\frac{\sum_{i=1}^k\tau_i^2}{k-1} & \tau_i: \text{ fixed, } \frac{\sum_{i=1}^k\tau_i^2}{k-1}\text{ donated by }\phi_\tau\\
(k-1)\sigma_\varepsilon^2+n(k-1)\sigma^2_{\tau} & \tau_i: \text{ random}
\end{cases}
\end{align*} ⟹ E ( S S t r t ) = { ( k − 1 ) σ ε 2 + n ∑ i = 1 k τ i 2 ( k − 1 ) σ ε 2 + n ( k − 1 ) σ τ 2 τ i : fixed τ i : random = { ( k − 1 ) σ ε 2 + n ( k − 1 ) k − 1 ∑ i = 1 k τ i 2 ( k − 1 ) σ ε 2 + n ( k − 1 ) σ τ 2 τ i : fixed, k − 1 ∑ i = 1 k τ i 2 donated by ϕ τ τ i : random
Fixed: ϕ τ = 0 ⟺ ∀ τ i = 0 ⟺ \phi_\tau=0\iff\forall\tau_i=0\iff ϕ τ = 0 ⟺ ∀ τ i = 0 ⟺
Random: σ τ 2 = 0 ⟺ \sigma_\tau^2=0\iff σ τ 2 = 0 ⟺
df of trt = k-1
M S t r t = S S t r t k − 1 ⟹ E ( M S t r t ) = { σ ε 2 + n ϕ τ τ i : fixed σ ε 2 + n σ τ 2 τ i : random MS_{trt}=\frac{SS_{trt}}{k-1}\implies E(MS_{trt})=\begin{cases}
\sigma^2_{\varepsilon}+n\phi_{\tau} & \tau_i: \text{ fixed}\\
\sigma^2_{\varepsilon}+n\sigma^2_{\tau} & \tau_i: \text{ random}
\end{cases} M S t r t = k − 1 S S t r t ⟹ E ( M S t r t ) = { σ ε 2 + n ϕ τ σ ε 2 + n σ τ 2 τ i : fixed τ i : random 我們對 trt 是否有效應感興趣,因此會檢驗:
H 0 : No trt effect v.s. H 1 : Sig. trt effect H_0: \text{ No trt effect v.s. } H_1: \text{ Sig. trt effect} H 0 : No trt effect v.s. H 1 : Sig. trt effect ⟺ H 0 : { ϕ τ = 0 σ τ 2 = 0 v.s. H 1 : { ϕ τ > 0 fixed σ τ 2 > 0 random \iff H_0:\begin{cases}
\phi_\tau=0 \\
\sigma^2_{\tau}=0
\end{cases}\quad\text{v.s. }\quad H_1:\begin{cases}
\phi_\tau > 0 & \text{ fixed}\\
\sigma^2_{\tau}> 0 & \text{ random}
\end{cases} ⟺ H 0 : { ϕ τ = 0 σ τ 2 = 0 v.s. H 1 : { ϕ τ > 0 σ τ 2 > 0 fixed random
Under H 0 H_0 H 0 ⟹ E ( M S E ) = σ ε 2 = E ( M S t r t ) \implies E(MS_E)=\sigma_\varepsilon^2=E(MS_{trt}) ⟹ E ( M S E ) = σ ε 2 = E ( M S t r t ) M S t r t MS_{trt} M S t r t M S E MS_E M S E
Under H 1 H_1 H 1 ⟹ E ( M S t r t ) = σ ε 2 + n ⋅ [ ϕ τ ∣ σ τ 2 ] > σ ε 2 = E ( M S E ) \implies E(MS_{trt})=\sigma_\varepsilon^2+n\cdot[\phi_\tau|\sigma_\tau^2]>\sigma_\varepsilon^2=E(MS_E) ⟹ E ( M S t r t ) = σ ε 2 + n ⋅ [ ϕ τ ∣ σ τ 2 ] > σ ε 2 = E ( M S E ) M S t r t MS_{trt} M S t r t M S E MS_E M S E
⟹ \implies ⟹ H 0 H_0 H 0 M S t r t > > M S E ⟺ MS_{trt}>>MS_E\iff M S t r t >> M S E ⟺ H 0 H_0 H 0 M S t r t / M S E > > 1 MS_{trt}/MS_E>>1 M S t r t / M S E >> 1
F ∗ ≜ M S t r t M S E ∼ H 0 F ( d f t r t , d f E ) = F k − 1 , N − k F^*\triangleq\frac{MS_{trt}}{MS_E}\overset{H_0}{\sim}F(df_{trt},df_E)=F_{k-1,N-k} F ∗ ≜ M S E M S t r t ∼ H 0 F ( d f t r t , d f E ) = F k − 1 , N − k REmark :
N − 1 = ( k − 1 ) + d f E ⟹ d f E = N − k = n k − k = k ( n − 1 ) N-1=(k-1)+df_E \implies df_E=N-k=nk-k=k(n-1) N − 1 = ( k − 1 ) + d f E ⟹ d f E = N − k = nk − k = k ( n − 1 ) Hence, reject H 0 H_0 H 0 α ⟺ \alpha \iff α ⟺
α = P ( reject H 0 ∣ H 0 is true ) = P H 0 ( F ∗ > F k − 1 , N − k , α ) \begin{align*}
\alpha&=P(\text{reject }H_0|H_0\text{ is true})\\
&=P_{H_0}(F^*>F_{k-1,N-k,\alpha})\\
\end{align*} α = P ( reject H 0 ∣ H 0 is true ) = P H 0 ( F ∗ > F k − 1 , N − k , α ) F l , m , α is s.t. P ( F l , m ≥ F l , m , α ) = α F_{l,m,\alpha} \text{ is s.t. }P(F_{l,m}\ge F_{l,m,\alpha})=\alpha F l , m , α is s.t. P ( F l , m ≥ F l , m , α ) = α ⟹ \implies ⟹ H 0 H_0 H 0 α ⟺ F ∗ > F k − 1 , N − k . α \alpha\iff F^*>F_{k-1,N-k.\alpha} α ⟺ F ∗ > F k − 1 , N − k . α F ∗ = M S t r t / M S E F^*=MS_{trt}/MS_E F ∗ = M S t r t / M S E
⟹ \implies ⟹
Source df SS MS=SS/df EMS=E(MS) F-value p-value trt k-1 S S t r t SS_{trt} S S t r t M S t r t MS_{trt} M S t r t σ ε 2 + n [ ϕ τ ∣ σ τ 2 ] \sigma_\varepsilon^2+n[\phi_\tau \mid \sigma_\tau^2] σ ε 2 + n [ ϕ τ ∣ σ τ 2 ] M S t r t / M S E = f ∗ MS_{trt}/MS_E=f^* M S t r t / M S E = f ∗ P ( F k − 1 , N − k > f ∗ ) P(F_{k-1,N-k}>f^*) P ( F k − 1 , N − k > f ∗ ) Error N-k S S E SS_E S S E M S E MS_E M S E σ ε 2 \sigma_\varepsilon^2 σ ε 2 Total N-1 S S t o t a l SS_{total} S S t o t a l
Note : k = 2 k=2 k = 2
⊥ < Y 11 , Y 12 , ⋯ , Y 1 n 1 ∼ N ( μ 1 , σ 2 ) Y 21 , Y 22 , ⋯ , Y 2 n 2 ∼ N ( μ 2 , σ 2 ) \perp\bigg<\begin{align*}
Y_{11},Y_{12},\cdots,Y_{1n_1}\sim N(\mu_1,\sigma^2)\\
Y_{21},Y_{22},\cdots,Y_{2n_2}\sim N(\mu_2,\sigma^2)
\end{align*} ⊥ ⟨ Y 11 , Y 12 , ⋯ , Y 1 n 1 ∼ N ( μ 1 , σ 2 ) Y 21 , Y 22 , ⋯ , Y 2 n 2 ∼ N ( μ 2 , σ 2 ) To test H 0 : μ 1 = μ 2 H_0:\mu_1=\mu_2 H 0 : μ 1 = μ 2 H 1 : μ 1 ≠ μ 2 H_1:\mu_1\neq\mu_2 H 1 : μ 1 = μ 2
∣ Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ( 1 n 1 + 1 n 2 ) S p 2 ∣ > t N − 2 , α / 2 with S p 2 = 1 n 1 + n 2 − 2 ( ∑ j = 1 n 1 ( Y 1 j − Y ˉ 1 ⋅ ) 2 + ∑ j = 1 n 2 ( Y 2 j − Y ˉ 2 ⋅ ) 2 ) \left|\frac{\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot}}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})S_p^2}}\right|>t_{N-2,\alpha/2}\qquad\text{with }S_p^2=\frac{1}{n_1+n_2-2}\left(\sum_{j=1}^{n_1}(Y_{1j}-\bar{Y}_{1\cdot})^2+ \sum_{j=1}^{n_2}(Y_{2j}-\bar{Y}_{2\cdot})^2\right) ( n 1 1 + n 2 1 ) S p 2 Y ˉ 1 ⋅ − Y ˉ 2 ⋅ > t N − 2 , α /2 with S p 2 = n 1 + n 2 − 2 1 ( j = 1 ∑ n 1 ( Y 1 j − Y ˉ 1 ⋅ ) 2 + j = 1 ∑ n 2 ( Y 2 j − Y ˉ 2 ⋅ ) 2 ) Note :
t ∗ ∼ H 0 t n 1 + n 2 − 2 = balanced if t n − 2 ≜ N ( 0 , 1 ) χ 2 n − 2 2 2 n − 2 > ⊥ t^*\overset{H_0}{\sim}t_{n_1+n_2-2}\xlongequal[\text{balanced}]{\text{if}}t_{n-2}\triangleq\frac{N(0,1)}{\sqrt{\frac{\chi^2_{2n-2}}{2n-2}}}\bigg>\perp t ∗ ∼ H 0 t n 1 + n 2 − 2 if balanced t n − 2 ≜ 2 n − 2 χ 2 n − 2 2 N ( 0 , 1 ) ⟩ ⊥ ⟹ ( t ∗ ) 2 ∼ H 0 ( t n − 2 ) 2 ∼ H 0 χ 1 2 / 1 χ 2 n − 2 2 / ( 2 n − 2 ) > ⊥ ∼ F 1 , 2 n − 2 = F 2 − 1 , N − 2 \implies (t^*)^2\overset{H_0}{\sim}(t_{n-2})^2\overset{H_0}{\sim}\frac{\chi^2_1/1}{\chi^2_{2n-2}/(2n-2)}\bigg>\perp\sim F_{1,2n-2}=F_{2-1,N-2} ⟹ ( t ∗ ) 2 ∼ H 0 ( t n − 2 ) 2 ∼ H 0 χ 2 n − 2 2 / ( 2 n − 2 ) χ 1 2 /1 ⟩ ⊥∼ F 1 , 2 n − 2 = F 2 − 1 , N − 2 if n 1 = n 2 = n n_1=n_2=n n 1 = n 2 = n
( t ∗ ) 2 = ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ( 1 n + 1 n ) S p 2 ) = ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) 2 2 n S p 2 = n 2 ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) 1 S p 2 = M S t r t M S E = F ∗ (t^*)^2=\left(\frac{\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot}}{\sqrt{(\frac{1}{n}+\frac{1}{n})S_p^2}} \right)=\frac{(\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot})^2}{\frac{2}{n}S_p^2}=\frac{n}{2}(\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot})\frac{1}{S_p^2}=\frac{MS_{trt}}{MS_E}=F^* ( t ∗ ) 2 = ( n 1 + n 1 ) S p 2 Y ˉ 1 ⋅ − Y ˉ 2 ⋅ = n 2 S p 2 ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) 2 = 2 n ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) S p 2 1 = M S E M S t r t = F ∗ M S t r t = S S t r t 2 − 1 = ∑ i = 1 2 ∑ j = 1 n ( Y ˉ i ⋅ − Y ˉ ⋅ ⋅ ) 2 = ∑ i = 1 2 n ( Y ˉ i ⋅ − 1 2 ( Y ˉ 1 ⋅ + Y ˉ 2 ⋅ ) ) 2 = n 2 ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) 2 \begin{align*}
MS_{trt}&=\frac{SS_{trt}}{2-1}=\sum_{i=1}^2\sum_{j=1}^n(\bar{Y}_{i\cdot}-\bar{Y}_{\cdot\cdot})^2\\
&=\sum_{i=1}^2n(\bar{Y}_{i\cdot}-\frac{1}{2}(\bar{Y}_{1\cdot}+\bar{Y}_{2\cdot}))^2\\
&=\frac{n}{2}(\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot})^2
\end{align*} M S t r t = 2 − 1 S S t r t = i = 1 ∑ 2 j = 1 ∑ n ( Y ˉ i ⋅ − Y ˉ ⋅⋅ ) 2 = i = 1 ∑ 2 n ( Y ˉ i ⋅ − 2 1 ( Y ˉ 1 ⋅ + Y ˉ 2 ⋅ ) ) 2 = 2 n ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) 2 S S E = ∑ i = 1 2 ∑ j = 1 n ( Y i j − Y ˉ i ⋅ ) 2 = ∑ j = 1 n ( Y 1 j − Y ˉ 1 ⋅ ) 2 + ∑ j = 1 n ( Y 2 j − Y ˉ 2 ⋅ ) 2 M S E = S S E N − k = S S E 2 n − 2 = S p 2 \begin{align*}
SS_E&=\sum_{i=1}^2\sum_{j=1}^n(Y_{ij}-\bar{Y}_{i\cdot})^2\\
&=\sum_{j=1}^n(Y_{1j}-\bar{Y}_{1\cdot})^2 + \sum_{j=1}^n(Y_{2j}-\bar{Y}_{2\cdot})^2\\
MSE&=\frac{SS_E}{N-k}=\frac{SS_E}{2n-2}=S_p^2
\end{align*} S S E MSE = i = 1 ∑ 2 j = 1 ∑ n ( Y ij − Y ˉ i ⋅ ) 2 = j = 1 ∑ n ( Y 1 j − Y ˉ 1 ⋅ ) 2 + j = 1 ∑ n ( Y 2 j − Y ˉ 2 ⋅ ) 2 = N − k S S E = 2 n − 2 S S E = S p 2 Paired data:
( Y 11 Y 21 ) , ( Y 12 Y 22 ) , ⋯ , ( Y 1 n Y 2 n ) ∼ iid N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) \begin{pmatrix}
Y_{11}\\
Y_{21}
\end{pmatrix},\begin{pmatrix}
Y_{12}\\
Y_{22}
\end{pmatrix},\cdots,\begin{pmatrix}
Y_{1n}\\
Y_{2n}
\end{pmatrix}\overset{\text{iid}}{\sim}N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho) ( Y 11 Y 21 ) , ( Y 12 Y 22 ) , ⋯ , ( Y 1 n Y 2 n ) ∼ iid N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) ⟹ \implies ⟹ H 0 : μ 1 = μ 2 H_0:\mu_1=\mu_2 H 0 : μ 1 = μ 2 H 1 : μ 1 ≠ μ 2 H_1:\mu_1\neq\mu_2 H 1 : μ 1 = μ 2
D j ≜ Y 1 j − Y 2 j , j = 1 , ⋯ , n ∼ iid N ( μ 1 − μ 2 , σ ε 2 ) , σ ε 2 = func of σ 1 2 , σ 2 2 , ρ D_j\triangleq Y_{1j}-Y_{2j},\quad j=1,\cdots,n\quad\overset{\text{iid}}\sim{N(\mu_1-\mu_2,\sigma^2_\varepsilon)},\quad\sigma^2_\varepsilon=\text{ func of }\sigma_1^2,\sigma_2^2,\rho D j ≜ Y 1 j − Y 2 j , j = 1 , ⋯ , n ∼ iid N ( μ 1 − μ 2 , σ ε 2 ) , σ ε 2 = func of σ 1 2 , σ 2 2 , ρ ∣ n D ˉ S D ∣ > t n − 1 , α / 2 ⟺ n D ˉ 2 S D 2 > F 1 , n − 1 , α ⟺ n 2 ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) ⏟ M S t r t 1 S D 2 / 2 > F 1 , n − 1 , α \left|\frac{\sqrt{n}\bar{D}}{S_D}\right|>t_{n-1,\alpha/2}\iff\frac{n\bar{D}^2}{S_D^2}>F_{1,n-1,\alpha}\iff \underbrace{\frac{n}{2}(\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot})}_{MS_{trt}}\frac{1}{S_D^2/2}>F_{1,n-1,\alpha} S D n D ˉ > t n − 1 , α /2 ⟺ S D 2 n D ˉ 2 > F 1 , n − 1 , α ⟺ M S t r t 2 n ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) S D 2 /2 1 > F 1 , n − 1 , α S D 2 ≜ 1 n − 1 ∑ j = 1 n ( D j − D ˉ ) 2 = 1 n − 1 ∑ j = 1 n [ ( Y 1 j − Y 2 j ) − ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) ] 2 \begin{align*}
S_D^2&\triangleq\frac{1}{n-1}\sum_{j=1}^n(D_j-\bar{D})^2\\
&=\frac{1}{n-1}\sum_{j=1}^n[(Y_{1j}-Y_{2j})-(\bar{Y}_{1\cdot}-\bar{Y}_{2\cdot})]^2\\
\end{align*} S D 2 ≜ n − 1 1 j = 1 ∑ n ( D j − D ˉ ) 2 = n − 1 1 j = 1 ∑ n [( Y 1 j − Y 2 j ) − ( Y ˉ 1 ⋅ − Y ˉ 2 ⋅ ) ] 2 Two-factor CRD with balanced
Y i j k = μ + A i + B j + A B i j + ε ( i j ) k i = 1 ⋯ a j = 1 ⋯ b k = 1 ⋯ n Y_{ijk}=\mu+A_i+B_j+AB_{ij}+\varepsilon_{(ij)k}\quad\begin{align*}
&i=1\cdots a\\
&j=1\cdots b\\
&k=1\cdots n
\end{align*} Y ijk = μ + A i + B j + A B ij + ε ( ij ) k i = 1 ⋯ a j = 1 ⋯ b k = 1 ⋯ n Number of trt = a b ab ab
Note : for fixed model, i.e. both A and B are fixed effect
⟹ ∑ i = 1 a A i = 0 , ∑ j = 1 b B j = 0 , ∀ j , ∑ i = 1 a A B i j = 0 = ∑ j = 1 b A B i j , ∀ i \implies\sum_{i=1}^aA_i=0,\quad\sum_{j=1}^bB_j=0,\quad\forall j, \sum_{i=1}^aAB_{ij}=0=\sum_{j=1}^bAB_{ij},\forall i ⟹ ∑ i = 1 a A i = 0 , ∑ j = 1 b B j = 0 , ∀ j , ∑ i = 1 a A B ij = 0 = ∑ j = 1 b A B ij , ∀ i
⟹ E ( S S E ) = E [ ∑ i = 1 a ∑ j = 1 b ∑ k = 1 n ( Y i j k − Y ˉ i j ⋅ ) 2 ] = E [ ∑ i ∑ j ∑ k ( μ + A i + B j + A B i j + ε i j k − μ − A i − B j − A B i j − ε ˉ i j ⋅ ) 2 ] = E [ ∑ i ∑ j ∑ k ( ε i j k − ε ˉ i j ⋅ ) 2 ] = a b ( n − 1 ) σ ε 2 \begin{align*}
\implies E(SSE)&=E\left[\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(Y_{ijk-\bar{Y}_{ij\cdot}})^2 \right]\\
&=E\left[\sum_i\sum_j\sum_k (\mu+A_i+B_j+AB_{ij}+\varepsilon_{ijk}-\mu-A_i-B_j-AB_{ij}-\bar{\varepsilon}_{ij\cdot})^2 \right]\\
&=E\left[\sum_i\sum_j\sum_k(\varepsilon_{ijk}-\bar{\varepsilon}_{ij\cdot})^2 \right]\\
&=ab(n-1)\sigma^2_{\varepsilon}
\end{align*} ⟹ E ( SSE ) = E [ i = 1 ∑ a j = 1 ∑ b k = 1 ∑ n ( Y ijk − Y ˉ ij ⋅ ) 2 ] = E [ i ∑ j ∑ k ∑ ( μ + A i + B j + A B ij + ε ijk − μ − A i − B j − A B ij − ε ˉ ij ⋅ ) 2 ] = E [ i ∑ j ∑ k ∑ ( ε ijk − ε ˉ ij ⋅ ) 2 ] = ab ( n − 1 ) σ ε 2 ⟹ E ( M S E ) = E ( S S E / [ a b ( n − 1 ) ] ) = σ ε 2 \implies E(MSE)=E(SSE/[ab(n-1)])=\sigma_\varepsilon^2 ⟹ E ( MSE ) = E ( SSE / [ ab ( n − 1 )]) = σ ε 2
E ( S S A ) ≜ E [ ∑ i ∑ j ∑ k ( Y ˉ i ⋅ ⋅ − Y ˉ ⋅ ⋅ ⋅ ) 2 ] = E [ ∑ i ∑ j ∑ k ( μ + A i + B ˉ ⋅ + A B ˉ i ⋅ + ε ˉ i ⋅ ⋅ − μ − A ˉ ⋅ − B ˉ ⋅ − A B ˉ ⋅ ⋅ − ε ˉ ⋅ ⋅ ⋅ ) 2 ] = ∑ i ∑ j ∑ k A i 2 − b n ⋅ E ( ∑ i = 1 a ( ε ˉ i ⋅ ⋅ − ε ˉ ⋅ ⋅ ⋅ ) 2 ) + 2 ∑ i ∑ j ∑ k A i E ( ε ˉ i ⋅ ⋅ − ε ˉ ⋅ ⋅ ⋅ ) ⏟ = 0 = b n ⋅ ∑ i A i 2 + b n σ ε 2 b n ( a − 1 ) = b n ( a − 1 ) ∑ i A i 2 a − 1 + ( a − 1 ) σ ε 2 , ∑ i A i 2 a − 1 + ( a − 1 ) donated by ϕ A \begin{align*}
E(SSA)&\triangleq E\left[\sum_i\sum_j\sum_k(\bar{Y}_{i\cdot\cdot}-\bar{Y}_{\cdot\cdot\cdot})^2 \right]\\
&=E\left[\sum_i\sum_j\sum_k(\mu+A_i+\bar{B}_\cdot+\bar{AB}_{i\cdot}+\bar{\varepsilon}_{i\cdot\cdot}-\mu-\bar{A}_\cdot-\bar{B}_\cdot-\bar{AB}_{\cdot\cdot}-\bar{\varepsilon}_{\cdot\cdot\cdot})^2\right]\\
&=\sum_i\sum_j\sum_k A_i^2-bn\cdot E(\sum_{i=1}^a(\bar{\varepsilon}_{i\cdot\cdot}-\bar{\varepsilon}_{\cdot\cdot\cdot})^2)+2\sum_i\sum_j\sum_k A_i\underbrace{E(\bar{\varepsilon}_{i\cdot\cdot}-\bar{\varepsilon}_{\cdot\cdot\cdot})}_{=0}\\
&=bn\cdot\sum_iA_i^2+bn\frac{\sigma_\varepsilon^2}{bn}(a-1)\\
&=bn(a-1)\frac{\sum_iA_i^2}{a-1}+(a-1)\sigma_\varepsilon^2,\quad \frac{\sum_iA_i^2}{a-1}+(a-1)\text{ donated by }\phi_A
\end{align*} E ( SS A ) ≜ E [ i ∑ j ∑ k ∑ ( Y ˉ i ⋅⋅ − Y ˉ ⋅⋅⋅ ) 2 ] = E [ i ∑ j ∑ k ∑ ( μ + A i + B ˉ ⋅ + A B ˉ i ⋅ + ε ˉ i ⋅⋅ − μ − A ˉ ⋅ − B ˉ ⋅ − A B ˉ ⋅⋅ − ε ˉ ⋅⋅⋅ ) 2 ] = i ∑ j ∑ k ∑ A i 2 − bn ⋅ E ( i = 1 ∑ a ( ε ˉ i ⋅⋅ − ε ˉ ⋅⋅⋅ ) 2 ) + 2 i ∑ j ∑ k ∑ A i = 0 E ( ε ˉ i ⋅⋅ − ε ˉ ⋅⋅⋅ ) = bn ⋅ i ∑ A i 2 + bn bn σ ε 2 ( a − 1 ) = bn ( a − 1 ) a − 1 ∑ i A i 2 + ( a − 1 ) σ ε 2 , a − 1 ∑ i A i 2 + ( a − 1 ) donated by ϕ A ⟹ E ( M S A ) = E ( S S A ) / ( a − 1 ) = b n ϕ A + σ ε 2 \implies E(MS_A)=E(SS_A)/(a-1)=bn\phi_A+\sigma_\varepsilon^2 ⟹ E ( M S A ) = E ( S S A ) / ( a − 1 ) = bn ϕ A + σ ε 2
Source df SS MS=SS/df EMS=E(MS) F-value p-value A a-1 SSA M S A MS_A M S A σ ε 2 + b n ϕ A \sigma_\varepsilon^2+bn\phi_A σ ε 2 + bn ϕ A M S A / M S E MS_A/MS_E M S A / M S E P ( F a − 1 , a b ( n − 1 ) > f ∗ ) P(F_{a-1,ab(n-1)}>f^*) P ( F a − 1 , ab ( n − 1 ) > f ∗ ) B b-1 SSB M S B MS_B M S B σ ε 2 + a n ϕ B \sigma_\varepsilon^2+an\phi_B σ ε 2 + an ϕ B M S B / M S E MS_B/MS_E M S B / M S E P ( F b − 1 , a b ( n − 1 ) > f ∗ ) P(F_{b-1,ab(n-1)}>f^*) P ( F b − 1 , ab ( n − 1 ) > f ∗ ) AB (a-1)(b-1) SSAB M S A B MS_{AB} M S A B σ ε 2 + n ϕ A B + \sigma_\varepsilon^2+n\phi_{AB}+ σ ε 2 + n ϕ A B + M S A B / M S E MS_{AB}/MS_E M S A B / M S E P ( F ( a − 1 ) ( b − 1 ) , a b ( n − 1 ) > f ∗ ) P(F_{(a-1)(b-1),ab(n-1)}>f^*) P ( F ( a − 1 ) ( b − 1 ) , ab ( n − 1 ) > f ∗ ) Error ab(n-1) SSE M S E MS_E M S E σ ε 2 \sigma_\varepsilon^2 σ ε 2 Total abn-1 SST
P A P_A P A H 0 H_0 H 0 ⟺ ϕ A = 0 \iff\phi_A=0 ⟺ ϕ A = 0 H 1 H_1 H 1 ⟺ ϕ A > 0 \iff\phi_A>0 ⟺ ϕ A > 0 P B P_B P B H 0 H_0 H 0 ⟺ ϕ B = 0 \iff\phi_B=0 ⟺ ϕ B = 0 H 1 H_1 H 1 ⟺ ϕ B > 0 \iff\phi_B>0 ⟺ ϕ B > 0 P A B P_{AB} P A B H 0 H_0 H 0 ⟺ ϕ A B = 0 \iff\phi_{AB}=0 ⟺ ϕ A B = 0 H 1 H_1 H 1 ⟺ ϕ A B > 0 \iff\phi_{AB}>0 ⟺ ϕ A B > 0
Note : M S A + M S B + M S A B = M S t r t MS_A+MS_B+MS_{AB}=MS_{trt} M S A + M S B + M S A B = M S t r t ( a − 1 ) + ( b − 1 ) + ( a − 1 ) ( b − 1 ) = a b − 1 = (a-1)+(b-1)+(a-1)(b-1)=ab-1= ( a − 1 ) + ( b − 1 ) + ( a − 1 ) ( b − 1 ) = ab − 1 =